已知函数 ,且
,且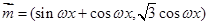 ,
,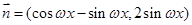 ,其中
,其中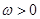 ,若函数
,若函数 相邻两对称轴的距离大于等于
相邻两对称轴的距离大于等于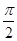 .
.
(1)求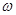 的取值范围;
的取值范围;
(2)在锐角三角形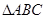 中,
中,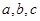 分别是角
分别是角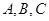 的对边,当
的对边,当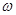 最大时,
最大时,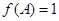 ,且
,且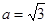 ,求
,求 的取值范围.
的取值范围.
从参加环保知识竞赛的学生中抽出60名,将其成绩整理后画出的频率分布直方图如下.观察图形,回答下列问题: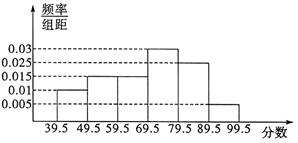
(1)49.5——69.5这一组的频率和频数分别为多少?
(2)估计这次环保知识竞赛成绩的中位数及平均成绩.(精确到小数点后一位)
 的取值范围为[0,10],给出如图所示程序框图,输入一个数
的取值范围为[0,10],给出如图所示程序框图,输入一个数 .
.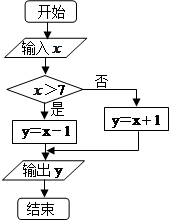
(1)请写出程序框图所表示的函数表达式;
(2)求输出的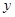 (
(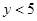 )的概率;(3)求输出的
)的概率;(3)求输出的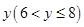 的概率.
的概率.
海关对同时从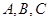 三个不同地区进口的某种商品进行抽样检测,从各地区进口此种商品的数量(单位:件)如下表所示,工作人员用分层抽样的方法从这些商品中共抽取6件进行检测.
三个不同地区进口的某种商品进行抽样检测,从各地区进口此种商品的数量(单位:件)如下表所示,工作人员用分层抽样的方法从这些商品中共抽取6件进行检测.
| 地区 |
 |
 |
 |
| 数量 |
50 |
150 |
100 |
(1)求这6件样品中来自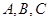 各地区商品的数量;
各地区商品的数量;
(2)若在这6件样品中随机抽取2件送往甲机构进一步检测,求这2件商品来自相同地区的概率.
在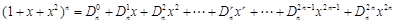 的展开式中,把
的展开式中,把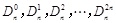 叫做三项式系数.
叫做三项式系数.
(1)当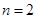 时,写出三项式系数
时,写出三项式系数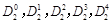 的值;
的值;
(2)类比二项式系数性质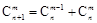
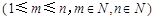 ,给出一个关于三项式系数
,给出一个关于三项式系数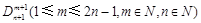 的相似性质,并予以证明;
的相似性质,并予以证明;
(3)求 的值.
的值.
(1)求证: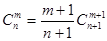 ;
;
(2)求和: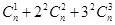
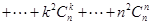 .
.