在某校组织的一次篮球定点投篮训练中,规定每人最多投  次;在
处每
投进一球得
次;在
处每
投进一球得  分,在
处每投进一球得
分,在
处每投进一球得 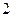 分;如果前两次得分之和超过
分;如果前两次得分之和超过  分即停止投篮,否则投第三次.同学在
处的命
分即停止投篮,否则投第三次.同学在
处的命  中率
为
中率
为 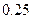 0,在
0,在
 处的命中率为
,该同学选择先在
处投一球,以后都在
处投,用
表示该同学投篮训练结束后所得的总分,其分布列为
处的命中率为
,该同学选择先在
处投一球,以后都在
处投,用
表示该同学投篮训练结束后所得的总分,其分布列为
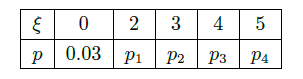
(1)求
的值; 
(2)求随  机变量
的数学期望
;
机变量
的数学期望
; 
(3)试比较该同学选择都在
处投篮得分超过3分与选择上述方式投篮得分超过3分的概率的大小.
某种食品是经过 、
、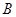 、
、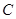 三道工序加工而成的,
三道工序加工而成的, 、
、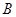 、
、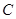 工序的产品合格率分别为
工序的产品合格率分别为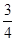 、
、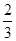 、
、 .已知每道工序的加工都相互独立,三道工序加工的产品都为合格时产品为一等品;有两道合格为二等品;其它的为废品,不进入市场.
.已知每道工序的加工都相互独立,三道工序加工的产品都为合格时产品为一等品;有两道合格为二等品;其它的为废品,不进入市场.
(1)正式生产前先试生产 袋食品,求这2袋食品都为废品的概率;
袋食品,求这2袋食品都为废品的概率;
(2)设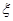 为加工工序中产品合格的次数,求
为加工工序中产品合格的次数,求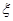 的分布列和数学期望.
的分布列和数学期望.
从一批苹果中,随机抽取50个,其重量(单位:克)的频数分布表如下:
| 分组(重量) |
 |
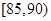 |
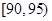 |
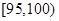 |
| 频数(个) |
5 |
10 |
20 |
15 |
(1)根据频数分布表计算苹果的重量在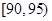 的频率;
的频率;
(2)用分层抽样的方法从重量在 和
和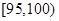 的苹果中共抽取4个,其中重量在
的苹果中共抽取4个,其中重量在 的有几个?
的有几个?
(3)在(2)中抽出的4个苹果中,任取2个,求重量在 和
和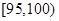 中各有1个的概率.
中各有1个的概率.
城市公交车的数量若太多则容易造成资源的浪费;若太少又难以满足乘客需求.某市公交公司在某站台的60名候车乘客中随机抽取15人,将他们的候车时间作为样本分成5组,如下表所示(单位:分钟):
| 组别 |
候车时间 |
人数 |
| 一 |
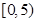 |
2 |
| 二 |
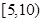 |
6 |
| 三 |
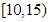 |
4 |
| 四 |
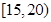 |
2 |
| 五 |
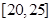 |
1 |
(1)估计这60名乘客中候车时间少于10分钟的人数;
(2)若从上表第三、四组的6人中任选2人作进一步的调查,求抽到的两人恰好来自不同组的概率.
2014年2月21日,《中共中央关于全面深化改革若干重大问题的决定》明确:坚持计划生育的基本国策,启动实施一方是独生子女的夫妇可生育两个孩子的政策.为了解某地区城镇居民和农村居民对“单独两孩”的看法,某媒体在该地区选择了3600人调查,就是否赞成“单独两孩”的问题,调查统计的结果如下表:
| 赞成 |
反对 |
无所谓 |
|
| 农村居民 |
2100人 |
120人 |
y人 |
| 城镇居民 |
600人 |
x人 |
z人 |
已知在全体样本中随机抽取1人,抽到持“反对”态度的人的概率为0.05.
(1)现在分层抽样的方法在所有参与调查的人中抽取360人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
(2)在持“反对”态度的人中,用分层抽样的方法抽取6人,按每组3人分成两组进行深入交流,求第一组中农村居民人数 的分布列和数学期望.
的分布列和数学期望.
已知正方形ABCD的边长为2,E,F,G,H分别是边AB,BC,CD,DA的中点.
(1)从C,D,E,F,G,H这六个点中,随机选取两个点,记这两个点之间的距离的平方为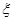 ,求概率P
,求概率P .
.
(2)在正方形ABCD内部随机取一点P,求满足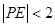 的概率.
的概率.