城市公交车的数量若太多则容易造成资源的浪费；若太少又难以满足乘客需求.某市公交公司在某站台的60名候车乘客中随机抽取15人，将他们的候车时间作为样本分成5组，如下表所示（单位：分钟）：
| 组别 |
候车时间 |
人数 |
| 一 |
 |
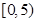2 |
| 二 |
 |
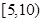6 |
| 三 |
 |
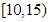4 |
| 四 |
 |
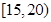2 |
| 五 |
 |
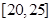1 |
（1）估计这60名乘客中候车时间少于10分钟的人数；
（2）若从上表第三、四组的6人中任选2人作进一步的调查，求抽到的两人恰好来自不同组的概率．
如图，在棱长为a的正方体ABCD－A1B1C1D1中，G为△BC1D的重心，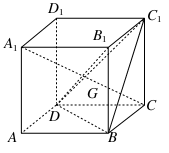
(1)求证：A1、G、C三点共线；
(2)求证：A1C⊥平面BC1D；
(3)求点C到平面BC1D的距离．
如图所示，已知空间四边形ABCD的每条边和对角线长都等于1，点E、F、G分别是AB、AD、CD的中点，计算：
(1)
·
；
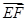(2)·
；
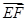(3)EG的长；
(4)异面直线AG与CE所成角的余弦值．
如图，已知矩形ABCD和矩形ADEF所在的平面互相垂直，点M，N分别在对角线BD，AE上，且BM＝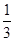
BD，AN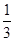＝AE.求证：MN∥平面CDE.
如图所示，在四棱锥P－ABCD中，四边形ABCD为菱形，△PAD为等边三角形，平面PAD⊥平面ABCD，且∠DAB＝60°，AB＝2，E为AD的中点．
(1)求证：AD⊥PB；
(2)求点E到平面PBC的距离．
在如图所示的几何体中，正方形ABCD和矩形ABEF所在的平面互相垂直，M为AF的中点，BN⊥CE.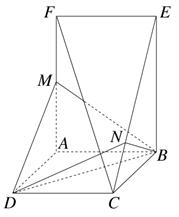
(1)求证：CF∥平面MBD；
(2)求证：CF⊥平面BDN.