(1)计算:|-2|+2sin30°-(-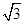 )2+(tan45°)-1.
)2+(tan45°)-1.
(2)先化简,再求值:2(a+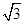 )(a-
)(a-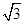 )-a(a-6)+6,其中a=
)-a(a-6)+6,其中a=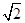 -1.
-1.
(本题8分)一个不透明的布袋里装有2个白球,1个黑球和若干个红球,它们除颜色外其余都相同,从中任意摸出1个球,是白球的概率为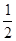 .
.
(1)布袋里红球有多少个?
(2)先从布袋中摸出1个球后不放回,再摸出1个球,请用列表或画树状图等方法求出两次摸到的球都是白球的概率.
(本小题满分12分)抛物线
 与x轴交于A ,B两点,且点A在点B的左侧,与y轴交于点C.
与x轴交于A ,B两点,且点A在点B的左侧,与y轴交于点C.
(1)当OB=OC时,求此时抛物线函数解析式;
(2)当△ABC为等腰三角形时,求m的值;
(3)若点P 与点Q
与点Q 在(1)中抛物线上,
在(1)中抛物线上, ,
, .求
.求 的值.
的值.
(本小题满分12分)某商场试销一种成本为每件60元的服装,规定试销期间销售单价不能低于成本单价,且获利不得高于成本的45%,经试销发现,销售量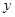 (件)与销售单价
(件)与销售单价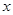 (元)符合一次函数
(元)符合一次函数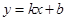 ,且
,且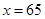 时,
时,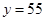 ;
;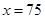 时,
时,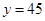 .
.
(1)求一次函数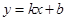 的表达式;
的表达式;
(2)若该商场获得利润为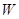 元,试写出利润
元,试写出利润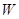 与销售单价
与销售单价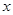 之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
(3)若该商场获得利润不低于500元,试确定销售单价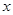 的范围.
的范围.
(本小题满分10分)已知关于x的函数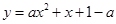 (a为常数).
(a为常数).
(1)若函数的图象与坐标轴恰有两个交点,求a的值;
(2)若函数的图象是抛物线,开口向上且顶点在x轴下方,求a的取值范围.
(本小题满分10分)如图所示,AB=AC,AB为⊙O的直径,AC、BC分别交⊙O于E、D,连结ED、BE.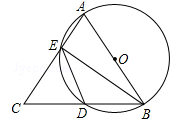
(1)试判断DE与BD是否相等,并说明理由;
(2)如果BC=6,AB=5,求BE的长.