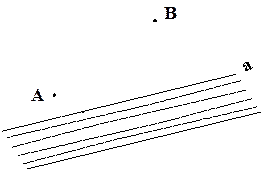因式分解:m3n-9mn.
如图所示,直线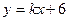 与
与 轴
轴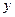 轴分别交于点E,
轴分别交于点E, F,点E的坐标为(-8,0),点A的坐标为(-6,0)。
F,点E的坐标为(-8,0),点A的坐标为(-6,0)。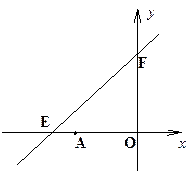
(1)求 的值;
的值;
(2)若点P(
 ,
,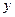 )是第二象限内的直线上的一个动点,当点P运动过程中,试写出△OPA的面积S与
)是第二象限内的直线上的一个动点,当点P运动过程中,试写出△OPA的面积S与 的函数关系式,并写出自变量
的函数关系式,并写出自变量 的取值范围;
的取值范围;
(3)当点P运动到什么位置时,△OPA的面积为 ?
?
如图,△ABC是等边三角形,BD是中线,延长BC至E,使CE= CD,求证:DB=DE
CD,求证:DB=DE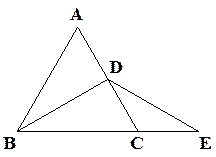
如果,AC⊥BC,BD⊥AD,AC=BD,求证BC=AD。
已知一次函数的图像经过点(-2,5),并且与直线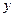 =3
=3 -4相交于
-4相交于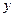
 轴上,求此函数的解析式
轴上,求此函数的解析式
如图,A、B是两个蓄水池,都在河边 的同侧,为了方便灌溉农作物,要在河边建一个抽水站,将河水送到A、B两地。问该站建在河边什么地方,可使所修
的同侧,为了方便灌溉农作物,要在河边建一个抽水站,将河水送到A、B两地。问该站建在河边什么地方,可使所修 的渠道最短?试
的渠道最短?试 在图中确定该点。(保留作图痕迹)
在图中确定该点。(保留作图痕迹)