如图,在平面直角坐标系xOy中,圆C:(x+1)2+y2=16,点F(1,0),E是圆C上的一个动点,EF的垂直平分线PQ与CE交于点B,与EF交于点D.
(1)求点B的轨迹方程;
(2)当点D位于y轴的正半轴上时,求直线PQ的方程;
(3)若G是圆C上的另一个动点,且满足FG⊥FE,记线段EG的中点为M,试判断线段OM的长度是否为定值?若是,求出该定值;若不是,说明理由.
如图所示,圆 的直径
的直径 ,
, 为圆周上一点,
为圆周上一点,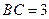 .过
.过 作圆的切线
作圆的切线 ,过
,过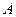 作
作 的垂线
的垂线 ,
, 分别与直线
分别与直线 、圆交于点
、圆交于点 ,求
,求 的度数和线段
的度数和线段 的长。
的长。
已知 ,
, .
.
(I)若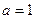 ,求
,求 ;
;
(II)若 R,求实数
R,求实数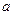 的取值范围
的取值范围
将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落.小球在下落过程中,将3次遇到黑色障碍物,最后落入A袋或B袋中.已知小球每次遇到黑色障碍物时向左、右两边下落的概率都是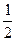 .
.
(Ⅰ)求小球落入A袋中的概率P(A);
(Ⅱ)在容器入口处依次放入4个小球,记X为落入A袋中小球的个数,试求X=3的概率和X的数学期望EX.
如图是一个方形迷宫,甲、乙两人分别位于迷宫的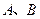 两处,两人同时以每一分钟一格的速度向东、西、南、北四个方向行走,已知甲向东、西行走的概率都为
两处,两人同时以每一分钟一格的速度向东、西、南、北四个方向行走,已知甲向东、西行走的概率都为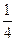 ,向南、北行走的概率为
,向南、北行走的概率为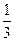 和
和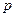 ,乙向东、西、南、北四个方向行走的概率均为
,乙向东、西、南、北四个方向行走的概率均为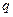
⑴求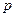 和
和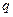 的值;
的值;
⑵问最少几分钟,甲、乙二人相遇?并求出最短时间内可以相遇的概率。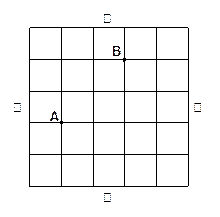
某大学开设甲、乙、丙三门选修课,学生是否选修哪门课互不影响. 已知某学生只选修甲的概率为0.08,只选修甲和乙的概率是0.12,至少选修一门的概率是0.88,用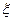 表示该学生选修的课程门数和没有选修的课程门数的乘积.
表示该学生选修的课程门数和没有选修的课程门数的乘积.
记“函数 为R上的偶函数”为事件A,求事件A的概率;
为R上的偶函数”为事件A,求事件A的概率;