某学校的篮球队、羽毛球队、乒乓球队各有10名队员,某些队员不止参加了一支球队,具体情况如图所示,现从中随机抽取一名队员,求:
(1)该队员只属于一支球队的概率;
(2)该队员最多属于两支球队的概率.
从4名书法比赛一等奖的同学和2名绘画比赛一等奖的同学中选出2名志愿者,参加某项服务工作.
(1)求选出的两名志愿者都是获得书法比赛一等奖的同学的概率;
(2)求选出的两名志愿者中一名是获得书法比赛一等奖,另一名是获得绘画比赛一等奖的同学的概率.
、对甲、乙的学习成绩进行抽样分析,各抽5门功课,得到的观测值如下:
| 甲 |
60 |
80 |
70 |
90 |
70 |
| 乙 |
80 |
60 |
70 |
80 |
75 |
问:甲、乙谁的平均成绩最好?谁的各门功课发展较平衡?
将一颗质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次,将得到的点数分别记为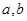 .
.
(1)求直线 与圆
与圆 相切的概率;
相切的概率;
(2)将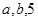 的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成
六段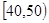 ,
,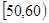 …
…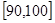 后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
(1)求第四小组的频率,并补全这个频率分布直方图;
(2)估计这次考试的及格率(60分及以上为及格)和平均分;
(3)用分层抽样的方法从成绩是80分以上(包括80分)的学生中抽取了6人进行试卷分析,再从这6个人中选2人作学习经验介绍发言,求选出的2人中至少有1人在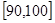 的概率.
的概率.
为了调查甲、乙两个网站受欢迎的程度,随机选取了 14天,统计上午8:00—10:00间各自的点击量,得如下所示的统计图,根据统计图:
(1)甲、乙两个网站点击量的极差分别是多少?
(2)甲网站点击量在[10,40]间的频率是多少?乙网站点击量的众数是多少?
(3)甲、乙两个网站哪个更受欢迎?并说明理由。