“抛阶砖”是国外游乐场的典型游戏之一.参与者只须将手上的“金币”(设“金币”的半径为1)抛向离身边若干距离的阶砖平面上,抛出的“金币”若恰好落在任何一个阶砖(边长为2.1的正方形)的范围内(不与阶砖相连的线重叠),便可获大奖.不少人被高额奖金所吸引,纷纷参与此游戏但很少有人得到奖品,请用所学的概率知识解释这是为什么.
一用户到电信局打算上网开户,经询问,有三种月消费方式:(1)163普通方式:上网资费2元/小时;(2)163A方式:每月30元(可上网50小时),超过50小时以上的资费为 2元/小时;(3) ADLSD方式:每月50元,时长不限(其它因素均忽略不计)。(每月以30日计算)
(1)、分别写出三种上网方式中所用月资费( )与时间(
)与时间(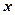 )的函数关系式;
)的函数关系式;
(2)、在同一坐标系内画出三种上网方式中所用资费与时间的函数图象;
(3)、根据你的研究,给这一用户一个合理化的建议。
已知圆的方程为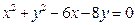 .圆内一点P
.圆内一点P
(1).若EF为过点P且倾斜角 =1350的弦,求EF的长;
=1350的弦,求EF的长;
(2).若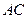 和
和 分别为过P
分别为过P 的最长弦和最短弦,求四边形
的最长弦和最短弦,求四边形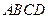 的面积。
的面积。
已知圆M:x2+y2-4y+3=0, Q是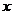 轴上的动点,QA、QB分别切圆M
轴上的动点,QA、QB分别切圆M
于A、B两点,(1)如果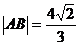 ,求点Q的坐标及直线MQ的方程;
,求点Q的坐标及直线MQ的方程;
(2)求动弦∣AB∣的最小值。
如图,在四面体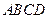 中,
中,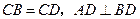 ,点
,点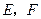 分别是
分别是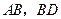 的中点.
的中点.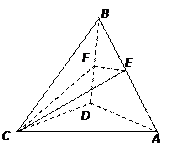
求证:(1)直线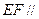 面
面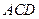 ;
;
(2)平面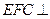 面
面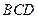 .
.
已知函数f(x)=

(1)、求f(2)与f( ),f(3)与f(
),f(3)与f( );
);
(2)、由(1)中求得结果,你能发现f(x) 与f(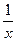 )有什么关系?并证明你的结论;
)有什么关系?并证明你的结论;
(3)、求f(1)+f(2)+f(3)+ 的值.
的值.