（1）如图1所示，固定于水平面上的金属框架abcd，处在竖直向下的匀强磁场中。金属棒MN沿框架以速度v向右做匀速运动。框架的ab与dc平行，bc与ab、dc垂直。MN与bc的长度均为l，在运动过程中MN始终与bc平行，且与框架保持良好接触。磁场的磁感应强度为B。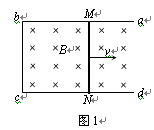
a. 请根据法拉第电磁感应定律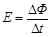
，推导金属棒MN中的感应电动势E；
b. 在上述情景中，金属棒MN相当于一个电源，这时的非静电力与棒中自由电子所受洛伦兹力有关。请根据电动势的定义，推导金属棒MN中的感应电动势E。
（2）为进一步研究导线做切割磁感线运动产生感应电动势的过程，现构建如下情景：如图2所示，在垂直于纸面向里的匀强磁场中，一内壁光滑长为l的绝缘细管MN，沿纸面以速度v向右做匀速运动。在管的N端固定一个电量为q的带正电小球（可看做质点）。某时刻将小球释放，小球将会沿管运动。已知磁感应强度大小为B，小球的重力可忽略。在小球沿管从N运动到M的过程中，求小球所受各力分别对小球做的功。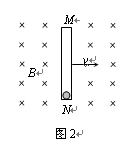
一种氢气燃料的汽车，质量为m = 2.0×103kg ，发动机的额定输出功率为P额="80kW" ，行驶在平直公路上时所受阻力恒为车重的0.1倍。若汽车从静止开始先匀加速启动，加速度的大小为a = 1.0m/s2。达到额定输出功率后，汽车保持功率不变又加速行驶了s="800m" ，直到获得最大速度后才匀速行驶。（g取10m/s2）。试求：
（1）汽车的最大行驶速度；
（2）汽车匀加速阶段结束时的速度；
（3）汽车以额定功率又加速了多长时间？
某战士在倾角θ = 30°的山坡上进行投掷手榴弹训练。他从A点以某一初速度υ0沿水平方向投出手榴弹，正好落在B点，测得AB 间的距离L= 90m。设空气阻力不计，取重力加速度g = 10m/s2。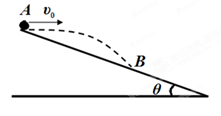
（1）该型号手榴弹从拉动弦到爆炸需要T=5s的时间，若要求手榴弹正好落地爆炸，求战士从拉动弦到投出所用时间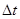
；
（2）求手榴弹抛出的初速度
大小。
如图，A容器容积为10 L，里面充满12 atm、温度为27℃的理想气体，B容器是真空。现将A中气体温度升高到400 K，然后打开阀门S，将A中的气体释放一部分到B容器，当A容器内压强降到4 atm时，关闭阀门，这时B容器内的压强是3 atm。不考虑气体膨胀过程中温度的变化，则B容器的容积为多大？ 
近来我国高速公路发生多起有关客车相撞的严重交通事故，原因之一就是没有掌握好车距，据经验丰富的司机总结，在高速公路上，一般可按你的车速来确定与前车的距离，如车速为80km/h，就应与前车保持80m的距离，以此类推，现有一辆客车以大小υ0 = 90km/h的速度行驶，一般司机反应时间t = 0.5s（反应时间内车被视为匀速运动），刹车时最大加速度a1 = 5m/s2。求：
（1）若司机发现前车因故突然停车，则从司机发现危险到客车停止运动，该客车通过的最短路程？并说明按经验，车距保持90m是否可行？
（2）若客车超载，刹车最大加速度减为a2 =" 4" m/s2；司机为赶时间而超速，速度达到υ1 = 144km/h；且晚上疲劳驾驶，反应时间增为t′ = 1.5s，则从司机发现危险到客车停止运动，客车通过的最短路程？并说明在此情况下经验是否可靠？
如图所示，将一块两面平行的玻璃砖平放在纸面上，将它的前、后两个边界PQ、MN记录在纸面上。若单色光沿纸面从真空中以入射角i＝60°，从MN表面射入时，光通过玻璃砖的时间为t；若保持入射光的方向不变，现撤去玻璃砖，光通过PQ、MN之间的区域的时间也为t，则这块玻璃砖对该入射光的折射率n为多大？