如图所示,直线l:y=3x+3与x轴交于点A,与y轴交于点B.把△AOB沿y轴翻折,点A落到点C,抛物线过点B、C和D(3,0).
(1)求直线BD和抛物线的解析式.
(2)若BD与抛物线的对称轴交于点M,点N在坐标轴上,以点N、B、D为顶点的三角形与△MCD相似,求所有满足条件的点N的坐标.
(3)在抛物线上是否存在点P,使S△PBD=6?若存在,求出点P的坐标;若不存在,说明理由.
某中学九年级数学兴趣小组为测量校内旗杆高度,如图,在C点测得旗杆顶端A的仰角为30°,向前走了6米到达D点,在D点测得旗杆顶端A的仰角为60°(测角器的高度不计).
(1) 米;
米;
(2)求旗杆AB的高度(结果保留1位小数, ).
).
小明和小亮用图中所示的转盘做游戏:分别转动转盘两次,若两次指针指向的数字之差(第一次数字减第二次的数字)大于或等于2,小明获胜,否则小亮获胜(指针恰好指在等分线上时重新转动转盤).
(1)分别求出小明和小亮得分的概率;
(2)你认为游戏是否公平?若公平,请说明理由.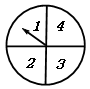
解不等式组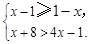 ,并求出它的整数解.
,并求出它的整数解.
如图,抛物线:y=ax2+bx+4与x轴交于点A(-2,0)和B(4,0)、与y轴交于点C.
(1)求抛物线的解析式;
(2)T是抛物线对称轴上的一点,且△ACT是以AC为底的等腰三角形,求点T的坐标;
(3)点M、Q分别从点A、B以每秒1个单位长度的速度沿x轴同时出发相向而行.当点M原点时,点Q立刻掉头并以每秒个单位长度的速度向点B方向移动,当点M到达抛物线的对称轴时,两点停止运动.过点M的直线l⊥轴,交AC或BC于点P.求点M的运动时间t(秒)与△APQ的面积S的函数关系式,并求出S的最大值.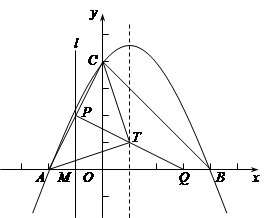
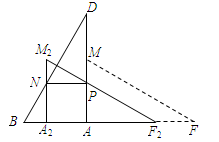
有两张完全重合的矩形纸片,小亮同学将其中一张绕点A顺时针旋转90°后得到矩形AMEF(如图),连结BD、MF,若此时他测得BD=8cm,∠ADB=30°.
(1)试探究线段BD与线段MF的关系,并简要说明理由;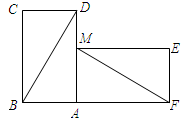
(2)小红同学用剪刀将△BCD与△MEF剪去,与小亮同学继续探究.他们将△ABD绕点A顺时针旋转得△AB1D1,AD1交FM于点K(如图),设旋转角为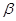 (0°<
(0°<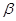 <90°),当△AFK为等腰三角形时,请直接写出旋转角
<90°),当△AFK为等腰三角形时,请直接写出旋转角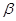 的度数;
的度数;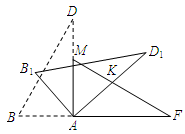
(3)若将△AFM沿AB方向平移得到△A2F2M2(如图),F2M2与AD交于点P,A2M2与BD交于点N,当NP∥AB时,求平移的距离是多少?