如图，抛物线：y＝ax2＋bx＋4与x轴交于点A(－2，0)和B(4，0)、与y轴交于点C．
(1)求抛物线的解析式；
(2)T是抛物线对称轴上的一点，且△ACT是以AC为底的等腰三角形，求点T的坐标；
(3)点M、Q分别从点A、B以每秒1个单位长度的速度沿x轴同时出发相向而行．当点M原点时，点Q立刻掉头并以每秒个单位长度的速度向点B方向移动，当点M到达抛物线的对称轴时，两点停止运动．过点M的直线l⊥轴，交AC或BC于点P．求点M的运动时间t(秒)与△APQ的面积S的函数关系式，并求出S的最大值．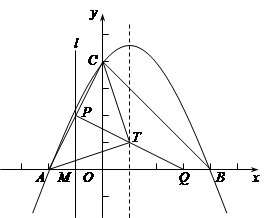
如图， AC与BD交于点E，且AC=DB，AB=DC．求证：∠A=∠D；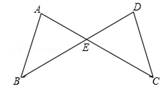
如图，已知直线l的函数表达式为
，且l与x轴、y轴分别交于A、B两点，动点Q从B点开始在线段BA上以每秒2个单位的速度向点A移动，同时动点P从A点开始在线段AO上以每秒1个单位的速度向O点移动，设点Q、P移动时间为t秒。
（1）求点A、B的坐标。
（2）当t为何值时，以点A、P、Q为顶点的三角形与△AOB相似？
如图所示，梯形ABCD中，AD∥BC，点E是边AD的中点，连接BE交AC于点F，BE的延长线交CD的延长线于点G。
（1）求证：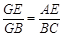
；
（2）若GE=2，BF=3，求线段EF的长。
如图，在△ABC中，∠BAC=90°，AB=AC，BE平分∠ABC，CE⊥BE，垂足为E．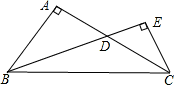
（1）求证：BD•BE=AB•BC；
（2）延长CE、BA交于F，求证：CF=BD．
如图，一位同学想利用影子测量旗杆的高度，在同一时刻，测得一米长的标杆的影长为1.2米，但他测旗杆影子时，因旗杆靠近教室，影子的一部分落在了墙上。他先测得地面部分的影子长为12米，又测得墙上影高为2米，求旗杆的高度AB。