如图所示,梯形ABCD中,AD∥BC,点E是边AD的中点,连接BE交AC于点F,BE的延长线交CD的延长线于点G。
(1)求证: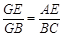 ;
;
(2)若GE=2,BF=3,求线段EF的长。
已知函数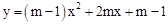 .
.
(1)m=时,函数图像与x轴只有一个交点;
(2)m为何值时,函数图像与x轴没有交点;
(3)若函数图像与x轴交于A、B两点,与y轴交于点C,且△ABC的面积为4,求m的值.
如图,直线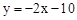 与
与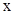 轴交于点A,直线
轴交于点A,直线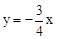 交于点B,点C在线段AB上,⊙C与
交于点B,点C在线段AB上,⊙C与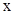 轴相切于点P,与OB切于点Q.
轴相切于点P,与OB切于点Q.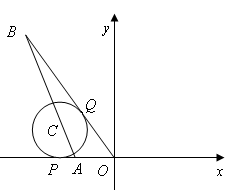
求:(1)A点的坐标;
(2)OB的长;
(3)C点的坐标.
某铝锭厂6月份生产铝锭7500吨,经过技术改革等改造,7月份生产铝锭8100吨,
(1)求7月份比6月份多生产铝锭产量的增长率;
(2)原来生产每吨铝锭耗电28.5度,经过两次改进工艺后,现在每吨耗电18.24吨,求两次耗电量下降的平均下降率?
已知二次函数图像与y轴交于点(0,-4),并经过(-1,-6)和(1,2)
(1)求这个二次函数的解析式;
(2)求出这个函数的图像的开口方向,对称轴和顶点坐标;
(3)该函数图像与x轴的交点坐标.
如图,AB为⊙O的直径,C为⊙O上的点,PA切于⊙O于点A,PA=PC,∠BAC=30°,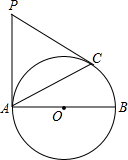
(1)求证:PC是⊙O的切线;
(2)若⊙O的半径为1,求PC的长(结果保留根号).