某创业投资公司拟投资开发某种新能源产品,估计能获得10万元到1000万元的投资收益.现准备制定一个对科研课题组的奖励方案:奖金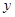 (单位:万元)随投资收益
(单位:万元)随投资收益 (单位:万元)的增加而增加,且奖金不超过9万元,同时奖金不超过投资收益的20%.
(单位:万元)的增加而增加,且奖金不超过9万元,同时奖金不超过投资收益的20%.
(1)若建立函数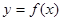 模型制定奖励方案,试用数学语言表述该公司对奖励函数
模型制定奖励方案,试用数学语言表述该公司对奖励函数 模型的基本要求,并分析函数
模型的基本要求,并分析函数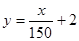 是否符合这个要求,并说明原因;
是否符合这个要求,并说明原因;
(2)若该公司采用函数 作为奖励函数模型,试确定最小的正整数
作为奖励函数模型,试确定最小的正整数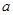 的值.
的值.
某地政府为科技兴市,欲将如图所示的一块不规则的非农业用地规划建成一个矩形的高科技工业园区.已知 ⊥
⊥ ,
,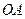 ∥
∥ ,且
,且 ,
,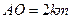 ,
, 曲线段
曲线段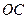 是以点
是以点 为顶
为顶 点且开口向上的抛物线的一段.如果要使矩形的相邻两边分别落
点且开口向上的抛物线的一段.如果要使矩形的相邻两边分别落
在 ,
, 上,且一个顶点落在曲线段
上,且一个顶点落在曲线段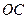 上.问:应如何规划才能使矩形工业园区的用地面积最大?并求出最大的用地面积(精确到
上.问:应如何规划才能使矩形工业园区的用地面积最大?并求出最大的用地面积(精确到 ).
).
已知抛物线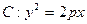 ,点
,点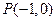 是其准线与
是其准线与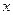 轴的焦点,过
轴的焦点,过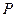 的直线
的直线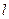 与抛物线
与抛物线 交于
交于 、
、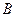 两点
两点 ,
, 为抛物线
为抛物线 的焦点.当线段
的焦点.当线段 的中点在直线
的中点在直线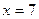 上时,求直线
上时,求直线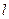 的方程,并求出此时
的方程,并求出此时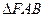 的面积.
的面积.
已知直线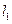 为曲线
为曲线 的切线,且与直线
的切线,且与直线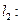
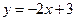 垂直.
垂直.
(1)求直线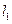 的方程;
的方程;
(2)求 由直线
由直线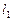 、
、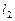 和
和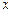 轴所围成的三角形
轴所围成的三角形 的面积.
的面积.
如图,已知三棱柱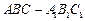 的侧棱与底面垂直,
的侧棱与底面垂直,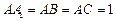 ,
,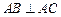 ,M是
,M是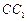 的中点,
的中点,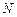 是
是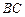 的中点,点
的中点,点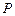 在
在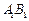 上,且满足
上,且满足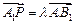 .
.
(1)证明: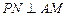 .
.
(2)当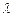 取何值时,直线
取何值时,直线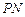 与平面
与平面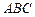 所成的角
所成的角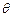 最大?并求该角最大值的正切值.
最大?并求该角最大值的正切值.
(3)若平面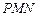 与平面
与平面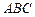 所成的二面角为
所成的二面角为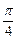 ,试确定P点的位置.
,试确定P点的位置.
过点(1,0)的直线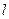 与中心在原点,焦点在x轴上且离心率为
与中心在原点,焦点在x轴上且离心率为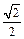 的椭圆C相
的椭圆C相 交于A、B两点,直线y=
交于A、B两点,直线y=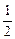 x过线段AB的中点,同时椭圆C上存在一点与其右焦点关于直线l
x过线段AB的中点,同时椭圆C上存在一点与其右焦点关于直线l 对称,试求直线l与椭圆C的方程
对称,试求直线l与椭圆C的方程