在平面直角坐标系xOy中,设椭圆C的中心在原点,焦点在x轴上,短半轴长为2,椭圆C上的点到右焦点的距离的最小值为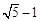 .
.
(1)求椭圆C的方程;
(2)设直线l与椭圆C相交于A,B两点,且 .
.
①求证:原点O到直线AB的距离为定值;
②求AB的最小值.
已知集合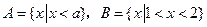 ,且
,且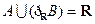 ,则实数
,则实数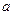 的取值范围
的取值范围
给出定义:若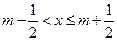 (其中
(其中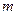 为整数),则
为整数),则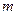 叫做离实数
叫做离实数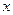 最近的整数,记作
最近的整数,记作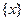 ,即
,即 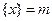 . 在此基础上给出下列关于函数
. 在此基础上给出下列关于函数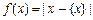 的四个命题:
的四个命题: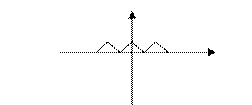
①函数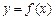 的定义域是R,值域是[0,
的定义域是R,值域是[0,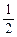 ];
];
②函数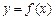 的图像关于直线
的图像关于直线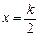 (k∈Z)对称;
(k∈Z)对称;
③函数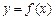 是周期函数,最小正周期是1;
是周期函数,最小正周期是1;
④函数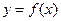 在
在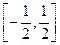 上是增函数;
上是增函数;
则其中真命题是__
(本小题满分14分)
设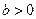 ,椭圆方程为
,椭圆方程为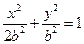 ,抛物线方程为
,抛物线方程为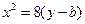 .如图6所示,过点
.如图6所示,过点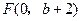 作
作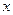 轴的平行线,与抛物线在第一象限的交点为
轴的平行线,与抛物线在第一象限的交点为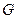 ,已知抛物线在点
,已知抛物线在点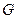 的切线经过椭圆的右焦点
的切线经过椭圆的右焦点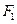 .
.
(1)求满足条件的椭圆方程和抛物线方程;
(2)设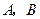 分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点
分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点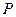 ,使得
,使得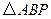 为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).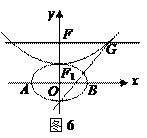
(本小题满分14分)
如图5所示,四棱锥 的底面
的底面 是半径为
是半径为 的圆的内接四边形,其中
的圆的内接四边形,其中 是圆的直径,
是圆的直径,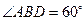 ,
,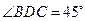 ,
, .
.
(1)求线段 的长;
的长;
(2)若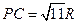 ,求三棱锥
,求三棱锥 的体积.
的体积.
(本小题满分14分)
设数列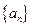 满足
满足 ,
,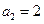 ,
, .数列
.数列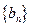 满足
满足 ,
, 是非零整数,且对任意的正整数
是非零整数,且对任意的正整数 和自然数
和自然数 ,都有
,都有 .
.
(1)求数列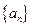 和
和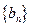 的通项公式;
的通项公式;
(2)记 ,求数列
,求数列 的前
的前 项和
项和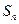 .
.