(本题10分)已知集合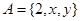 ,
, ,若
,若 ,求实数
,求实数 、
、 的值.
的值.
一份航空意外伤害保险保险费为20元,保险金额为45万元.如果某城市的一家保险公司一年能销售这种保单10万份,所需成本为5万元,而需要赔付的概率为 .那么请问1年内赔付人数为多少时,这家保险公司会亏本?
.那么请问1年内赔付人数为多少时,这家保险公司会亏本?
一台仪器每启动一次都随机地出现一个5位二进制数
| A1 |
A2 |
A3 |
A4 |
A5 |
A=
其中A1=1,Ak(k=2,3,4,5)为0的概率为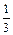 ,为1的概率为
,为1的概率为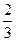 .例如若A=10001,其中A1= A5=1,A2= A3= A4=0.记m= A1+A2+ A3+ A4+ A5,求启动仪器一次时,
.例如若A=10001,其中A1= A5=1,A2= A3= A4=0.记m= A1+A2+ A3+ A4+ A5,求启动仪器一次时,
(1)P(m="3)" (2)P(m≤3)
有外形相同的球分装三个盒子,每盒10个,其中,第一个盒子中7个球标有字母A,3个球标有字母B;第二个盒子中有红球和白球各5个;第三个盒子中则有红球8个,白球2个.试验按如下规则进行:先在第一个盒子中任取一球,若取得标有字母A的球,则在第二个盒子中任取一球;若第一次取得标有字母B的球,则在第三个盒子中任取一球.若第二次取出的是红球,则称试验成功.求试验成功的概率.
用A、B、C三类不同的元件连接成两个系统N1、N2当元件A、B、C都正常工作时,系统N1正常工作,当元件A正常工作且元件B、C至少有一个正常工作时,系统N2正常工作。已知元件A、B、C正常工作的概率依次为0.80, 0.90, 0.90,分别求系统N1、N2正常工作的概率.
 |
|
 |
在n(n>3)次独立重复试验中,每次试验中某事件A发生的概率是P,求第3次事件A发生所需要的试验次数 的分布列.
的分布列.