如图,三棱柱ABC—A1B1C1的侧棱AA1⊥底面ABC,∠ACB = 90°,E是棱CC1上中点,F是AB中点,AC = 1,BC = 2,AA1 = 4.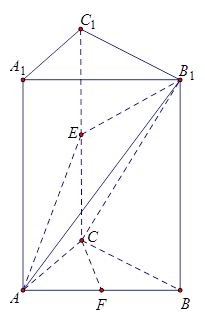
(1)求证:CF∥平面AEB1;(2)求三棱锥C-AB1E的体积.
已知定义在R上的函数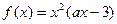 ,其中a为常数.
,其中a为常数.
(1)若x=1是函数 的一个极值点,求a的值;
的一个极值点,求a的值;
(2)若函数 在区间(-1,0)上是增函数,求a的取值范围;
在区间(-1,0)上是增函数,求a的取值范围;
(3)若函数 ,在x=0处取得最大值,求正数a的取值范围.
,在x=0处取得最大值,求正数a的取值范围.
设数列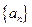 满足
满足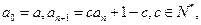 其中
其中 为实数,且
为实数,且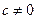
(Ⅰ)求数列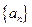 的通项公式
的通项公式
(Ⅱ)设 ,
,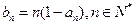 ,求数列
,求数列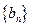 的前
的前 项和
项和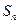 ;
;
(Ⅲ)若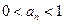 对任意
对任意 成立,证明
成立,证明
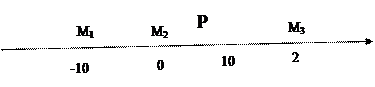
已知3台机器位于直线l上,机器所在的位置如下图所示,其中 M1 M2 ="10m," M2 M3 =20m;现要放置一台检验台P,用函数方法确定放在哪里可使检验台P到3台机器的距离和最小?
|




设函数 ,曲线
,曲线 在点
在点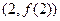 处的切线方程
处的切线方程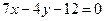 。
。
(1)求 的解析式;
的解析式;
(2)证明:曲线 上任一点处的切线与直线
上任一点处的切线与直线 和直线
和直线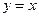 所围成的三角形面积为定值,并求此定值。
所围成的三角形面积为定值,并求此定值。
若 ,求函数f(x)=
,求函数f(x)=  的值域.
的值域.