如图所示,在四棱锥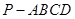 中,底面四边形
中,底面四边形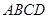 是菱形,
是菱形,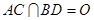 ,
,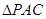 是边长为2的等边三角形,
是边长为2的等边三角形,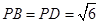 ,
,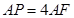 .
.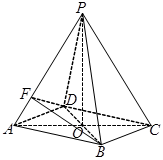
(1)求证: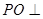 底面
底面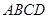 ;
;
(2)求直线 与平面
与平面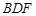 所成角的大小;
所成角的大小;
(3)在线段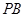 上是否存在一点
上是否存在一点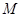 ,使得
,使得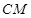 ∥平面
∥平面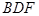 ?如果存在,求
?如果存在,求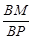 的值,如果不存在,请说明理由.
的值,如果不存在,请说明理由.
(本小题满分12分)
如图,某观测站C在城A的南偏西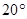 的方向,从城A出发有一条走向为南偏东
的方向,从城A出发有一条走向为南偏东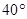 的公路,在C处观测到距离C处31km的公路上的B处有一辆汽车正沿公路向A城驶去,行驶了20km后到达D处,测得C,D两处的距离为21km,这时此车距离A城多少千米?
的公路,在C处观测到距离C处31km的公路上的B处有一辆汽车正沿公路向A城驶去,行驶了20km后到达D处,测得C,D两处的距离为21km,这时此车距离A城多少千米?
(本小题满分12分)已知函数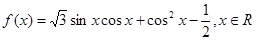
(1)求函数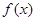 的最小正周期和单调增区间;
的最小正周期和单调增区间;
(2)作出函数在一个周期内的图象。
已知二项式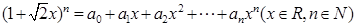
(1)若展开式中第五项的二项式系数是第三项系数的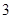 倍,求
倍,求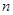 的值;
的值;
(2)若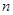 为正偶数时,求证:
为正偶数时,求证: 为奇数.
为奇数.
(3)证明: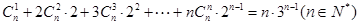
把正整数按从小到大顺序排列成下列数表,数表中第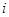 行共有
行共有 个正整数:
个正整数: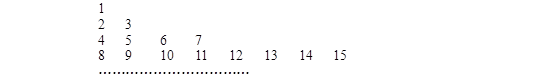
设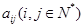 是位于数表中从上往下数第
是位于数表中从上往下数第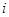 行、从左往右数第
行、从左往右数第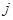 个数
个数
(1)若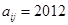 ,求
,求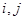 的值;
的值;
(2)记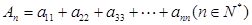 ,求数列
,求数列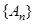 的通项公式;
的通项公式;
(3)猜想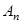 与
与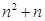 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
已知正方体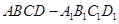 的棱长为1,点
的棱长为1,点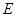 在
在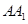 上,点
上,点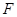 在
在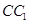 上,且
上,且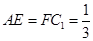
(1)求直线 与平面
与平面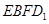 所成角的余弦值;
所成角的余弦值;
(2)用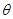 表示平面
表示平面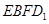 和侧面
和侧面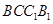 所成的锐二面角的大小,求
所成的锐二面角的大小,求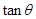 ;
;
(3)若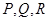 分别在
分别在 上,并满足
上,并满足 ,探索:当
,探索:当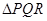 的重心为
的重心为 且
且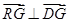 时,求实数
时,求实数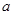 的取值范围.
的取值范围.