为了倡导健康、低碳、绿色的生活理念，某市建立了公共自行车服务系统鼓励市民租用公共自行车出行公共自行车按每车每次的租用时间进行收费，具体收费标准如下：
①租用时间不超过1小时，免费；
②租用时间为1小时以上且不超过2小时，收费1元；
③租用时间为2小时以上且不超过3小时，收费2元；
④租用时间超过3小时的时段，按每小时2元收费（不足1小时的部分按1小时计算）已知甲、乙两人独立出行，各租用公共自行车一次，两人租车时间都不会超过3小时，设甲、乙租用时间不超过1小时的概率分别是0.4和0.5 ，租用时间为1小时以上且不超过2小时的概率分别是0.5和0.3.
（1）求甲、乙两人所付租车费相同的概率；
（2）设甲、乙两人所付租车费之和为随机变量
，求的分布列和数学期望E
已知箱子中有10个球，期中8个是正品，2个是次品，若每次取出1个球，取出后不放回，求：
（1）取两次就能取到2个正品的概率；
（2）取三次才能取到2个正品的概率；
（3）取四次才能取到2个正品的概率.
函数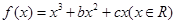
,已知
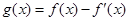是奇函数.
（1）求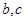
的值；
（2）求
的单调区间；
（3）求的极值.
7名师生站成一排照相留念,其中老师1人,男生4人,女生2人,在下列情况下,各有不同站法多少种？
（1）两名女生必须相邻而站；
（2）4名男生互不相邻；
（3）若4名男生身高都不等,按从高到低的顺序站；
（4）老师不站中间,女生不站两端.
已知在
的展开式中，前三项的系数成等差数列.
（1）求
；
（2）求展开式中的常数项；
（3）求展开式中系数最大的项.
已知复数
.
（1）求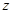
的实部与虚部；
（2）若
（
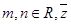是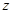的共轭复数），求
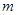和
的值.