对于函数 ,若在定义域存在实数
,若在定义域存在实数 ,满足
,满足 ,则称
,则称 为“局部奇函数”.
为“局部奇函数”.
(1)已知二次函数 ,试判断
,试判断 是否为“局部奇函数”?并说明理由;
是否为“局部奇函数”?并说明理由;
(2)设 是定义在
是定义在 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数 的取值范围.
的取值范围.
(本小题满分12分)
已知向量 =(sinA,cosA),
=(sinA,cosA), 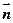 =
= ,
, ,且A为锐角.
,且A为锐角.
(1)求角A的大小;
(2)求函数 的值域.
的值域.
(本小题满分12分)
已知函数 .
.
(1)若点
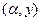 (
(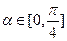 )为函数
)为函数 与
与 的图象的公共点,试求实数
的图象的公共点,试求实数 的值;
的值;
(2)设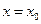 是函数
是函数 的图象的一条对称轴,求
的图象的一条对称轴,求 的值;
的值;
(3)求函数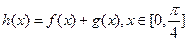 的值域。
的值域。
(本小题满分12分) 已知△ABO中,延长BA到C,使AC="BA," D是将
已知△ABO中,延长BA到C,使AC="BA," D是将 分成
分成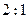 的一个分点,DC和OA交于E,设
的一个分点,DC和OA交于E,设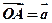 ,
,
(1)用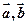 表示向量
表示向量 。
。
(2)若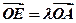 ,求实数
,求实数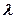 的值。
的值。
(本小题满分12分)
设函数f(x)=cos(2x+ )+sin
)+sin x.
x.
(1)求函数f(x)的最小值及取得最小值时x的值。
(2)设A,B,C为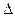 ABC的三个内角,若cosB=
ABC的三个内角,若cosB= ,
, ,且C为锐角,求sinA.
,且C为锐角,求sinA.
(本小题满分10分)
已知函数f (x)=a+bsinx+2cosx(x∈R)的图象经过点A(0,1),B .
.
(1)求函数f (x)的单调递减区间;
(2)由函数y=f (x)的图象经过平移是否能得到一个奇函数y=g(x)的图象?若能,请写出平移过程;若不能,请说明理由.