(本小题满分12分)
设函数f(x)=cos(2x+ )+sin
)+sin x.
x.
(1)求函数f(x)的最小值及取得最小值时x的值。
(2)设A,B,C为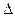 ABC的三个内角,若cosB=
ABC的三个内角,若cosB= ,
, ,且C为锐角,求sinA.
,且C为锐角,求sinA.
(本小题满分10分)选修4-4:坐标系与参数方程
已知椭圆C: ,直线
,直线 (t为参数).
(t为参数).
(Ⅰ)写出椭圆C的参数方程及直线 的普通方程;
的普通方程;
(Ⅱ)设 ,若椭圆C上的点P满足到点A的距离与其到直线
,若椭圆C上的点P满足到点A的距离与其到直线 的距离相等,求点P的坐标.
的距离相等,求点P的坐标.
(本小题满分10分)如图,圆周角 的平分线与圆交于点D,过点D的切线与弦AC的延长线交于点E,AD交BC于点F.
的平分线与圆交于点D,过点D的切线与弦AC的延长线交于点E,AD交BC于点F.
(Ⅰ)求证: ;
;
(Ⅱ)若D,E,C,F四点共圆,且弧长AC等于弧长BC,求 .
.
(本小题满分12分)已知函数 ,
, .
.
(Ⅰ)若函数 在定义域上是增函数,求a的取值范围;
在定义域上是增函数,求a的取值范围;
(Ⅱ)求 的最大值.
的最大值.
(本小题满分12分)已知圆 ,点
,点 ,以线段AB为直径的圆内切于圆
,以线段AB为直径的圆内切于圆 ,记点B的轨迹为
,记点B的轨迹为 .
.
(Ⅰ)求曲线 的方程;
的方程;
(Ⅱ)直线AB交圆 于C,D两点,当B为CD中点时,求直线AB的方程.
于C,D两点,当B为CD中点时,求直线AB的方程.
(本小题满分12分)如图,在斜三棱柱 中,侧面
中,侧面 与侧面
与侧面 都是菱形,
都是菱形, ,
, .
.
(Ⅰ)求证: ;
;
(Ⅱ)若 ,求四棱锥
,求四棱锥 的体积.
的体积.