已知三点 ,
, ,
, .
.
(1)求 与
与 的夹角;
的夹角;
(2)求 在
在 方向上的投影.
方向上的投影.
定义在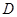 上的函数
上的函数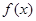 ,如果满足:对任意
,如果满足:对任意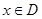 ,存在常数
,存在常数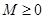 ,都有
,都有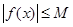 成立,则称
成立,则称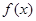 是
是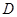 上的有界函数,其中
上的有界函数,其中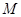 称为函数
称为函数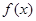 的一个上界.
的一个上界.
已知函数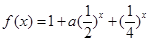 ,
,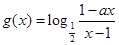 .
.
(1)若函数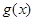 为奇函数,求实数
为奇函数,求实数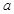 的值;
的值;
(2)在(1)的条件下,求函数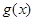 在区间
在区间 上的所有上界构成的集合;
上的所有上界构成的集合;
(3)若函数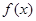 在
在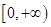 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数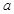 的取值范围.
的取值范围.
已知圆 的方程:
的方程: ,其中
,其中 .
.
(1)若圆C与直线 相交于
相交于 ,
, 两点,且
两点,且 ,求
,求 的值;
的值;
(2)在(1)条件下,是否存在直线 ,使得圆上有四点到直线
,使得圆上有四点到直线 的距离为
的距离为 ,若存在,求出
,若存在,求出 的范围,若不存在,说明理由.
的范围,若不存在,说明理由.
如图所示,圆锥的轴截面为等腰直角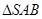 ,
,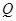 为底面圆周上一点.
为底面圆周上一点.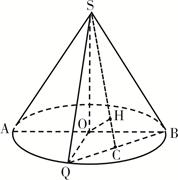
(1)若 的中点为
的中点为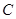 ,
, ,
,
求证: 平面
平面 ;
;
(2)如果 ,
,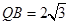 ,求此圆锥的全面积.
,求此圆锥的全面积.
已知幂函数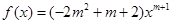 为偶函数.
为偶函数.
(1)求 的解析式;
的解析式;
(2)若函数 在区间(2,3)上为单调函数,求实数
在区间(2,3)上为单调函数,求实数 的取值范围.
的取值范围.