在直角坐标系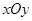 中,曲线
中,曲线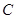 的参数方程为
的参数方程为 为参数),以该直角坐标系的原点
为参数),以该直角坐标系的原点 为极点,
为极点,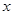 轴的正半轴为极轴的极坐标系下,曲线
轴的正半轴为极轴的极坐标系下,曲线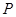 的方程为
的方程为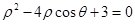 .
.
(1)求曲线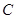 的普通方程和曲线
的普通方程和曲线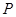 的直角坐标方程;
的直角坐标方程;
(2)设曲线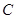 和曲线
和曲线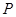 的交点为
的交点为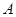 、
、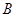 ,求
,求 .
.
(本小题满分12分)如图,在长方体ABCD-A1B1C1D1中,AD=AAl=1,AB=2,点E在棱AB上移动.
(I)证明:D1E上AlD;
(Ⅱ)当E为AB的中点时,求点E到面ACD1的距离;
(Ⅲ)在(II)的条件下,求D1E与平面AD1C所成角的正弦值.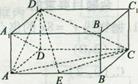
(本小题满分12分)已知a∈(0,6),b∈(0,6)
(I)求∣a-b∣≤1的概率;
(Ⅱ)以a,b作为直角三角形两直角边的边长,则斜边长小于6的概率.
(本小题满分12分)一个车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了4次试验.收集的数据如下: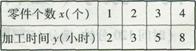
(I)请画出上表数据的散点图;
(Ⅱ)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程 ;
;
(Ⅲ)现需生产20件此零件,预测需用多长时间?
(注:用最小二乘法求线性回归方程系数公式 )
)
(本小题满分12分)动圆C截直线3x-y=0和3x+y=0所得弦长分别为8、4,求动圆圆心C的轨迹方程.
(本小题满分10分)从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如下,观察图形,回答下列问题.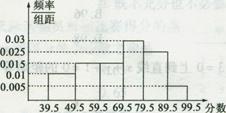
(I)在79.5~89.5之间的频率、频数分别是多少?
(Ⅱ)估计这次环保知识竞赛的及格率(60分及以上为及格).