已知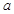 、
、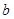 、
、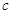 为正实数,
为正实数,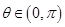 .
.
(1)当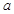 、
、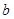 、
、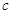 为
为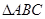 的三边长,且
的三边长,且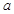 、
、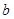 、
、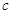 所对的角分别为
所对的角分别为 、
、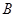 、
、 .若
.若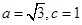 ,且
,且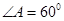 .求
.求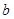 的长;
的长;
(2)若 .试证明长为
.试证明长为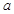 、
、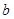 、
、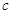 的线段能构成三角形,而且边
的线段能构成三角形,而且边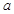 的对角为
的对角为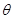 .
.
如图,在棱长为a的正方体ABCD-A1B1C1D1中,G为△BC1D的重心,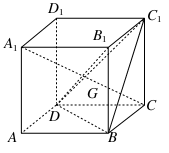
(1)求证:A1、G、C三点共线;
(2)求证:A1C⊥平面BC1D;
(3)求点C到平面BC1D的距离.
如图所示,已知空间四边形ABCD的每条边和对角线长都等于1,点E、F、G分别是AB、AD、CD的中点,计算:
(1)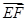 ·
· ;
;
(2)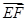 ·
· ;
;
(3)EG的长;
(4)异面直线AG与CE所成角的余弦值.
如图,已知矩形ABCD和矩形ADEF所在的平面互相垂直,点M,N分别在对角线BD,AE上,且BM=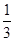 BD,AN=
BD,AN=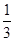 AE.求证:MN∥平面CDE.
AE.求证:MN∥平面CDE.
如图所示,在四棱锥P-ABCD中,四边形ABCD为菱形,△PAD为等边三角形,平面PAD⊥平面ABCD,且∠DAB=60°,AB=2,E为AD的中点.
(1)求证:AD⊥PB;
(2)求点E到平面PBC的距离.
在如图所示的几何体中,正方形ABCD和矩形ABEF所在的平面互相垂直,M为AF的中点,BN⊥CE.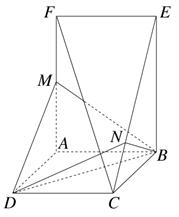
(1)求证:CF∥平面MBD;
(2)求证:CF⊥平面BDN.