(14分)如图所示,木板与水平地面间的夹角θ可以随意改变,当θ=30°时,可视为质点的一小木块恰好能沿着木板匀速下滑。若让该小木块从木板的底端以大小恒定的初速率v0=10m/s的速度沿木板向上运动,随着θ的改变,小物块沿木板滑行的距离x将发生变化,重力加速度g=10m/s2。(结果可用根号表示)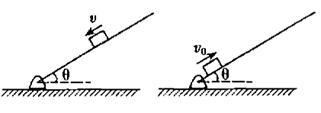
(1)求小物块与木板间的动摩擦因数;
(2)当θ角满足什么条件时,小物块沿木板滑行的距离最小,并求出此最小值。
“∟”形轻杆两边互相垂直、长度均为l,可绕过O点的水平轴在竖直平面内自由转动。两端各固定一个金属小球A、B;其中A球质量为m、带负电、电荷量为q(q > 0);B球不带电,质量为 m。重力加速度为g 。现将“∟”形杆从OB位于水平位置由静止释放。已知sin37°=0.6,cos37°=0.8。求:
m。重力加速度为g 。现将“∟”形杆从OB位于水平位置由静止释放。已知sin37°=0.6,cos37°=0.8。求:
(1)A、B两球的最大动能之和为多少?
(2)若在空间加竖直向下的匀强电场,OB杆仍从原来位置释放后,能转过的最大角度为127°,则该电场的电场强度大小为多少?
如图所示,两根质量均为m、电阻均为R、长度均为l的导体棒a、b,用两条等长的、质量和电阻均可忽略的、不可伸长的柔软长直导线连接后,b放在距地面足够高的光滑绝缘水平桌面上,a靠在桌子的光滑绝缘侧面上;两根导体棒均与桌子边缘平行。整个空间存在水平向右的匀强磁场,磁感应强度为B。开始时两棒静止,自由释放后开始运动,导体棒a在落地前就已匀速运动,此时导体棒b仍未离开桌面。已知两条导线除桌边拐弯处外其余部位均处于伸直状态,导线与桌子侧棱间无摩擦。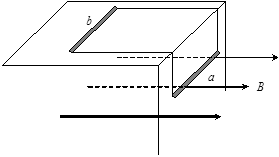
(1)试求导体棒匀速运动时的速度大小。
(2)从自由释放到刚匀速运动的过程中,若通过导体棒横截面的电荷量为q,求该过程中系统产生的焦耳热。
如图所示,在平面直角坐标系xOy中,第Ⅰ象限内有平行于 轴的匀强电场,方向沿y轴正方向;第Ⅳ象限的正三角形abc区域内有匀强磁场,方向垂直于xOy平面向里。正三角形边长为L,且
轴的匀强电场,方向沿y轴正方向;第Ⅳ象限的正三角形abc区域内有匀强磁场,方向垂直于xOy平面向里。正三角形边长为L,且 边与y轴平行。质量为m、电荷量为q的粒子,从y轴上的P(0,h)点,以大小为v0的速度沿x轴正方向射入电场,通过电场后从x轴上的a(2h,0)点进入第Ⅳ象限,又经过磁场从y轴上的某点进入第Ⅲ象限,且速度与y轴负方向成45°角,不计粒子所受的重力。试求:
边与y轴平行。质量为m、电荷量为q的粒子,从y轴上的P(0,h)点,以大小为v0的速度沿x轴正方向射入电场,通过电场后从x轴上的a(2h,0)点进入第Ⅳ象限,又经过磁场从y轴上的某点进入第Ⅲ象限,且速度与y轴负方向成45°角,不计粒子所受的重力。试求:
(1)电场强度的大小。
(2)粒子到达a点时速度的大小和方向。
(3)△abc区域内磁场的磁感应强度的最小值。
如图所示,质量M = 4.0kg的木板长L =" 2.0" m,静止在水平地面上,木板与地面间的动摩擦因数为μ1=0.05。木板水平上表面左端静置质量m =" 2.0" kg的小滑块(可视为质点),小滑块与板间的动摩擦因数为μ2 = 0.2。从某时刻开始,用F="5.0" N的水平力一直向右拉滑块,直至滑块滑离木板。设木板与地面间的最大静摩擦力等于滑动摩擦力,取g ="10" m/s2。试求:
(1)此过程中木板的位移大小。
(2)滑块离开木板时的速度大小。
如图所示,在xoy坐标系第一象限内有匀强磁场,磁场区域上边界刚好与直线y=a重合,磁感应强度为B。一个带正电的离子在坐标为(a,0)的A点以某一速度进入磁场区域,进入磁场时速度方向与x轴正向夹角为30°,离子质量为m,带电量为q。不计离子重力。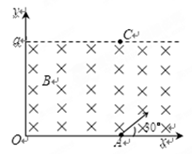
(1)若离子离开磁场时位置坐标为(a,a )的C点,求离子运动的速度大小?
(2)当离子进入磁场的速度满足什么条件时可使离子在磁场区域运动的时间最长?并求出最长时间是多少?