给定椭圆 :
: ,称圆心在原点
,称圆心在原点 ,半径为
,半径为 的圆是椭圆
的圆是椭圆 的“准圆”.若椭圆
的“准圆”.若椭圆 的一个焦点为
的一个焦点为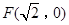 ,其短轴上的一个端点到
,其短轴上的一个端点到 的距离为
的距离为 .
.
(1)求椭圆 的方程和其“准圆”方程;
的方程和其“准圆”方程;
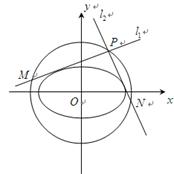
(2)点 是椭圆
是椭圆 的“准圆”上的动点,过点
的“准圆”上的动点,过点 作椭圆的切线
作椭圆的切线 交“准圆”于点
交“准圆”于点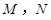 .
.
(ⅰ)当点 为“准圆”与
为“准圆”与 轴正半轴的交点时,求直线
轴正半轴的交点时,求直线 的方程并证明
的方程并证明 ;
;
(ⅱ)求证:线段 的长为定值.
的长为定值.
已知函数 ,当
,当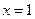 时,有极大值
时,有极大值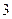 ;
;
(1)求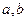 的值;(2)求函数
的值;(2)求函数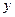 的极小值。
的极小值。
求函数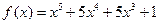 在区间
在区间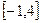 上的最大值与最小值。
上的最大值与最小值。
求函数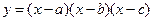 的导数。
的导数。
对某校小学生进行心理障碍测试得如下列联表:(其中焦虑、说谎、懒惰都是心理障碍)
| 焦虑 |
说谎 |
懒惰 |
总计 |
|
| 女生 |
5 |
10 |
15 |
30 |
| 男生 |
20 |
10 |
50 |
80 |
| 总计 |
25 |
20 |
65 |
110 |
试说明在这三种心理障碍中哪一种与性别关系最大?
一机器可以按各种不同的速度运转,其生产物件有一些会有缺点,每小时生产有缺点物件的多少随机器运转速度而变化,用x表示转速(单位:转/秒),用y表示每小时生产的有缺点物件个数,现观测得到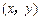 的4组观测值为(8,5),(12,8),(14,9),(16,11).
的4组观测值为(8,5),(12,8),(14,9),(16,11).
(1)假定y与x之间有线性相关关系,求y对x的回归直线方程;
(2)若实际生产中所容许的每小时最大有缺点物件数为10,则机器的速度不得超过多少转/秒.(精确到1转/秒)