如图所示,某市政府决定在以政府大楼 为中心,正北方向和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地,并考虑与周边环境协调,设计要求该图书馆底面矩形的四个顶点都要在边界上,图书馆的正面要朝市政府大楼.设扇形的半径
为中心,正北方向和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地,并考虑与周边环境协调,设计要求该图书馆底面矩形的四个顶点都要在边界上,图书馆的正面要朝市政府大楼.设扇形的半径 ,
, ,
, 与
与 之间的夹角为
之间的夹角为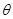 .
.
(1)将图书馆底面矩形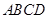 的面积
的面积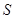 表示成
表示成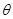 的函数.
的函数.
(2)求当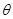 为何值时,矩形
为何值时,矩形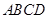 的面积
的面积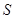 有最大值?其最大值是多少?(用含R的式子表示)
有最大值?其最大值是多少?(用含R的式子表示)
(本小题满分12分)已知幂函数 的图象经过点
的图象经过点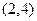 ,对于偶函数
,对于偶函数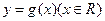 ,当
,当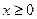 时,
时,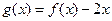 。
。
(1)求函数 的解析式;
的解析式;
(2)求当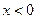 时,函数
时,函数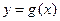 的解析式,并在给定坐标系下,画出函数
的解析式,并在给定坐标系下,画出函数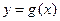 的图象
的图象
(3)写出函数 的单调递减区间
的单调递减区间
(本小题满分12分)
已知集合
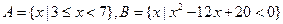 ,
, 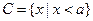 .
.
(1)求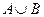 ;
;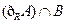
(2)若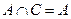 ,求
,求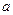 的取值范围
的取值范围
(本小题满分14分
函数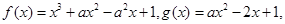 实数
实数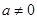 .
.
(I)若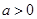 ,求函数
,求函数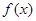 的单调区间;
的单调区间;
(II)当函数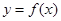 与
与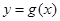 的图象只有一个公共点且
的图象只有一个公共点且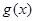 存在最小值时,记
存在最小值时,记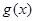 的最小值为
的最小值为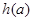 ,求的值域;
,求的值域;
(III)若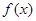 与
与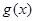 在区间
在区间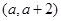 内均为增函数,求
内均为增函数,求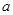 的取值范围。
的取值范围。
(文)已知函数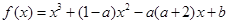
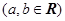 .
.
(I)若函数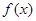 的图象过原点,且在原点处的切线斜率是
的图象过原点,且在原点处的切线斜率是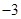 ,求
,求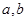 的值;
的值;
(II)若函数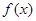 在区间
在区间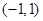 上不单调,求
上不单调,求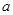 的取值范围
的取值范围
(本小题满分12分)
数列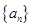 满足
满足
(1)求数列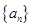 的通项公式;
的通项公式;
(2)令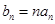 ,求数列的前n
,求数列的前n 项和
项和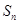
(本小题满分12分)
已知 是等比数列,
是等比数列,  ,
,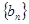 是等差数列,
是等差数列,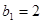
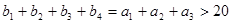
(1)求数列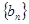 的通项公式;
的通项公式;
(2)求数列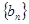 的前n项和
的前n项和 ;
;
(3)设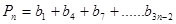 ,
, 其中n=1,2,......,试比较
其中n=1,2,......,试比较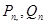 的大小。
的大小。