如图,已知点 是离心率为
是离心率为 的椭圆
的椭圆 :
:
 上的一点,斜率为
上的一点,斜率为 的直线
的直线 交椭圆
交椭圆 于
于 ,
,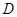 两点,且
两点,且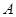 、
、 、
、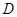 三点互不重合.
三点互不重合.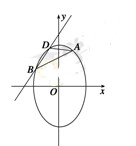
(1)求椭圆 的方程;(2)求证:直线
的方程;(2)求证:直线 ,
, 的斜率之和为定值.
的斜率之和为定值.
((本小题12分)
设函数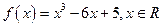
(1)若关于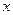 的方程
的方程 有三个不同的实根,求实数
有三个不同的实根,求实数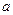 的取值范围。
的取值范围。
(2)当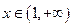 时,
时,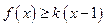 恒成立。求实数
恒成立。求实数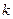 的取值范围。
的取值范围。
((本小题12分)
设函数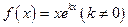
(1)求曲线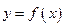 在点
在点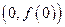 处的切线方程。
处的切线方程。
(2)若函数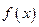 在区间
在区间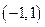 内单调递增,求
内单调递增,求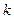 的取值范围。
的取值范围。
((本小题满分12分)
如图,四棱锥S—ABCD的底面是边长为1的正方形,SD垂直于底面ABCD,SB= .
.
(Ⅰ)求面ASD与面BSC所成二面角的大小;
(Ⅱ)设棱SA的中点为M,求异面直线DM与
SB所成角的大小;
(Ⅲ)求点D到平面SBC的距离.
((本小题满分12分)
已知椭圆的中心在坐标原点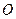 ,焦点在
,焦点在 轴上,椭圆的短轴端点和焦点所组成的四边形为正方形,短轴长为2.
轴上,椭圆的短轴端点和焦点所组成的四边形为正方形,短轴长为2.
(Ⅰ)求椭圆的方程;
(Ⅱ)设直线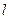 过
过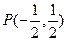 且与椭圆相交于A,B两点,当P是AB的中点时,
且与椭圆相交于A,B两点,当P是AB的中点时,
求直线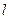 的方程.
的方程.
(本小题满分12分)
设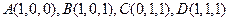 ,求直线AD与平面
,求直线AD与平面 的夹
的夹 角。
角。