（1）某同学得用气垫导轨和数字计数器探究弹簧的弹性势能与形变量的关系。如图所示，气垫导轨上有很多小孔，气泵输入压缩空气，从小孔中喷出，会使质量为
滑块与导轨间有一层薄的空气，使二者不接触从而减小阻力，一端固定有轻弹簧滑块在导轨上滑行，当通过数字计数器时，遮光片档住光源，与光敏管相连的电子电路就会记录遮光时间
。
①接通气泵，调节气垫导轨左端高度，轻推滑块，使其刚好能够匀速运动，说明气垫导轨已调节水平。
②使用10分度的游标卡尺，测量滑块上遮片的宽度如图乙所示，其宽度为
cm。
③压缩弹簧并记录压缩量。
④释放滑块，滑块离开弹簧后通过数字计时器显示时间。
⑤多次重复步骤③和④，将数据记录在表格中，并计算出滑块相应的速度。表格中弹簧压缩4.00cm时，其物块速度
m/s（保留三位有效数字）。
⑥从表格中的数据可以得出（在误差允许的范围内）弹簧的压缩量与物块的速度 。
⑦由机械守恒定律可知滑块的动能等于释放滑块时弹簧的弹性势能。
⑧由以上分析可得出弹簧的弹性势能与弹簧的压缩量关系表达式为 ，
其中各符号代表的物理意义 。
（2）某课外活动小组自制了一台称重电子秤，其原理结构如图甲图所示，R0为定值电阻；R是压敏电阻，其阻值随所受压力F的变化而变化，变化范围大约为几欧到几十欧，通过电压表的读数可以知道压力大小。若要想电子秤正常工作，首先通过实验探究压敏电阻阻值和F大小的关系，于是课外小组又设计了如图乙所示的探究压敏电阻阻值和F大小的关系的实验电路。图乙电路中由下列主要实验器材进行选择：
| A．电源E（3V，内阻忽略不计） |
| B．电流表A1（0.3A，内阻r1=10Ω） |
| C．电流表A2（0.6A，内阻约为1Ω） |
| D．电压表V（15V，内阻约为5kΩ） |
E．开关S，定值电阻R1
①为了比较准确测量电阻R，请完成图乙虚线框里两块表的选择（填电表代号）。
②图乙中，在电阻R上施加竖直向下的力F，闭合开关S，记录各个电表读数，得出R= ，表达式中需要测量的各字母的物理意义为
。
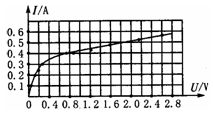
③图乙所示电路中，改变力的大小，得到不同的R值，得到如图丙所示的R—F图象，写出R和F的关系式R= 。
④若甲图所示的电路中，在压敏电阻R上水平放置一个重力为1.0N的托盘，在托盘上放一重物，电源电动势E=9.0V，电源内阻r=1.0Ω，R0=5.0Ω，闭合开关，电压表示数为5.0V，则重物的重量为 N。
某学生利用“研究匀变速直线运动”的实验装置来测量一个质量m="50" g的重锤下落时的加速度值，该学生将重锤固定在纸带下端，让纸带穿过打点计时器，实验装置如图所示.以下是该同学正确的实验操作和计算过程，请填写其中的空白部分:
(1)实验操作:应先___________，后释放纸带，让重锤自由落下， 实验结束后应立即___________.
(2)取下纸带，取其中的一段标出计数点如图所示，测出相邻计数点间的距离分别为x1="2.60" cm，x2="4.14" cm，x3="5.69" cm，x4="7.22" cm，x5="8.75" cm，x6="10.29" cm，已知打点计时器的打点间隔T="0.02" s，则重锤运动的加速度计算表达式为a=_____________，代入数据，可得加速度a=______________m/s2(计算结果保留三位有效数字).
| x1/cm |
x2/cm |
x3/cm |
x4/cm |
| 8.20 |
9.30 |
10.40 |
11.50 |
在“描绘小灯泡的伏安特性曲线”的实验中，可供选择的器材及代号如下：
A．小灯泡L（3V、5Ω）；
B．滑动变阻器R（0－10Ω，额定电流1.5A）；
C．电压表V1（量程：0－3V，R V ＝5kΩ）；
D．电压表V2（量程：0－15V，R V ＝10kΩ）；
E．电流表A1（量程：0－0.6A，R A ＝0.5Ω）；
F．电流表A2（量程：0－3A，R A ＝0.1Ω）；
G．铅蓄电池、开关各一个，导线若干；
实验中要求加在小灯泡两端的电压可连续地从零调到额定电压。
（1）为了减少误差，实验中应选电压表 ，电流表 ；
（2）在实验中，电流表应采用 法（填“内接”或“外接”）；
（3）请在图虚线框内按要求设计实验电路图（部分线已画好）
（4）某同学实验后作出的I－U 图象如图所示，请分析该图象形成的原因是： 。
“验证力的平行四边形定则”的实验情况如图甲所示，其中A为固定橡皮筋的图钉，O为橡皮筋与细绳结点，OB和OC为细绳。图乙是在白纸上根据实验结果画出的图。
（1）本实验采用的科学方法是
| A．理想实验法 | B．等效替代法 |
| C．控制变量法 | D．建立物理模型法 |
（2）某同学用两个弹簧秤将结点拉至某位置，此时该同学记录下了结点O的位置及两弹簧秤对应的读数，他还应该记录下___________________________。
（3）图乙中的F是利用平行四边定则作出的两个弹簧秤拉力的合力的图示，F'为用一个弹簧秤将结点拉至同一点时所用拉力的图示，这两个力中，方向一定沿AO方向的是____________。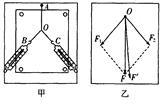
在“研究匀变速直线运动”的实验中，小车拖着纸带的运动情况如图所示，图中
、
、
、
、
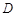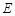为相邻的计数点，相邻的两个计数点间有4个实际打的点未画出，标出的数据单位是cm，则打点计时器打点与打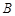点的时间间隔为 s，打点计时器在打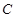点时小车的瞬时速度为 m/s，小车运动的加速度为 m/s2.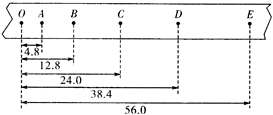
如图是“研究匀变速直线运动”实验中得到的一条纸带，从O点开始每5个点取一个计数点（打点计时器的电源频率是50Hz），依照打点的先后依次编为1、2、3、4、5、6，量得
1=2.21cm， 2=3.00cm，3=3.81cm，4=4.63cm，5=5.45cm，6=6.28cm。
（1）该打点计时器依次打出各计数点的时间间隔为T= s
（2）打点计时器打计数点5时，小车的速度大小是v 5= m/s。（结果保留两位有效数字）
（3）为了尽量减小实验误差，利用该实验数据计算出小车的加速度大小为a = m/s2（结果保留两位有效数字）。