已知某种零件的尺寸X(单位:mm)服从正态分布,其正态曲线在(0,80)上是增函数,在(80,+∞)上是减函数,且f(80)= .
.
(1)求正态分布密度函数的解析式;
(2)估计尺寸在72mm~88mm之间的零件大约占总数的百分之几.
在△ 中,角
中,角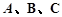 的对边分别为
的对边分别为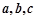 ,
,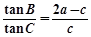 .
.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)求函数
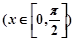 的值域
的值域
已知数列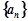 的前
的前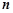 项和为
项和为 ,
,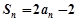 .
.
(Ⅰ)求数列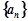 的通项公式;
的通项公式;
(Ⅱ)设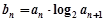 ,求数列
,求数列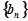 的前
的前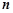 项和
项和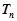 .
.
已知二次函数h(x)=ax2+bx+c(其中c<3),其导函数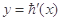 的图象如图,f(x)=6lnx+h(x)
的图象如图,f(x)=6lnx+h(x)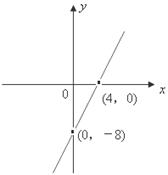
(1)求f(x)在x=3处的切线斜率;
(2)若f(x)在区间(m,m+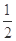 )上是单调函数,求实数m的取值范围;
)上是单调函数,求实数m的取值范围;
(3)若对任意k∈[-1,1],函数y=kx(x∈(0,6])的图象总在函数y=f(x)图象的上方,求c的取值范围
设函数
(1)当 时,求
时,求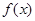 的单调区间;
的单调区间;
(2)若当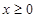 时
时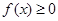 恒成立,求实数
恒成立,求实数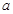 的取值范围。
的取值范围。
如图所示,某饲养场要建造一间两面靠墙的三角形露天养殖场,已知已有两面墙的夹角为60°(即 ),现有可供建造第三面围墙的材料60米(两面墙的长均大于60米),为了使得小老虎能健康成长,要求所建造的三角形露天活动室尽可能大,记
),现有可供建造第三面围墙的材料60米(两面墙的长均大于60米),为了使得小老虎能健康成长,要求所建造的三角形露天活动室尽可能大,记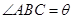 ,
,
(1)问当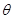 为多少时,所建造的三角形露天活动室的面积最大?
为多少时,所建造的三角形露天活动室的面积最大?
(2)若饲养场建造成扇形,养殖场的面积能比(1)中的最大面积更大?说明理由。