在某市组织的一次数学竞赛中全体参赛学生的成绩近似服从正态分布N(60,100),已知成绩在90分以上(含90分)的学生有13人.
(1)求此次参加竞赛的学生总数共有多少人?
(2)若计划奖励竞赛成绩排在前228名的学生,问受奖学生的分数线是多少?
设双曲线的顶点为 ,该双曲线又与直线
,该双曲线又与直线 交于
交于 两点,且
两点,且 (
( 为坐标原点)。
为坐标原点)。
(1)求此双曲线的方程;
(2)求
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB= ,AF=1,M是线段EF的中点.
,AF=1,M是线段EF的中点.
(Ⅰ)求证AM//平面BDE;
(Ⅱ)求二面角A-DF-B的大小;
(Ⅲ)试在线段AC上确定一点P,使得PF与BC所成的角是60°.
已知:以点C (t,  )(t∈R , t ≠ 0)为圆心的圆与
)(t∈R , t ≠ 0)为圆心的圆与 轴交于点O, A,与y轴交于点O, B,其中O为原点.
轴交于点O, A,与y轴交于点O, B,其中O为原点.
(Ⅰ)求证:△OAB的面积为定值;
(Ⅱ)设直线y = –2x+4与圆C交于点M, N,若|OM| = |ON|,求圆C的方程.
已知函数 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,有
时,有 (其中
(其中 为自然对数的底,
为自然对数的底, ).
).
(1)求函数 的解析式;
的解析式;
(2)设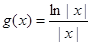 ,
,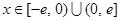 ,求证:当
,求证:当 时,
时, ;
;
(3)试问:是否存在实数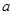 ,使得当
,使得当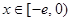 时,
时, 的最小值是3?如果存在,求出实数
的最小值是3?如果存在,求出实数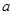 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
设函数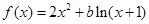 ,其中
,其中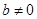 .
.
(1)当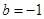 时,求在曲线
时,求在曲线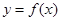 上一点
上一点 处的切线方程;
处的切线方程;
(2)求函数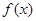 的极值点。
的极值点。