甲、乙两人参加某电视台举办的答题闯关游戏,按照规则,甲先从6道备选题中一次任意抽取3道题,独立作答,然后由乙回答剩余3题,每人答对其中的2题就停止答题,即闯关成功。已知6道备选题中,甲能答对其中的4道题,乙答对每道题的概率都是 .
.
(1)求甲、乙至少有一人闯关成功的概率;
(2)设甲答对题目的个数为 ,求
,求 的分布列及数学期望.
的分布列及数学期望.
如图,已知三棱柱 的侧棱与底面垂直,且
的侧棱与底面垂直,且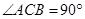 ,
, ,
,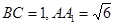 ,点
,点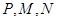 分别为
分别为 、
、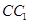 、
、 的中点.
的中点.
(1)求证: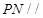 平面
平面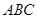 ;
;
(2)求证: ;
;
(3)求二面角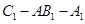 的余弦值.
的余弦值.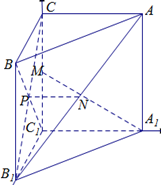
在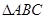 中,角
中,角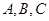 所对的边分别为
所对的边分别为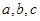 ,已知
,已知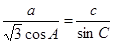 ,
,
(1)求 的大小;
的大小;
(2)若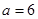 ,求
,求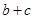 的取值范围.
的取值范围.
如图,已知圆心坐标为 的圆
的圆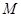 与
与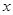 轴及直线
轴及直线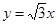 均相切,切点分别为
均相切,切点分别为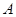 、
、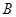 ,另一圆
,另一圆 与圆
与圆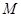 、
、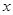 轴及直线
轴及直线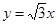 均相切,切点分别为
均相切,切点分别为 、
、 。
。
(1)求圆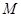 和圆
和圆 的方程;
的方程;
(2)过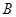 点作
点作 的平行线
的平行线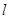 ,求直线
,求直线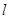 被圆
被圆 截得的弦的长度;
截得的弦的长度;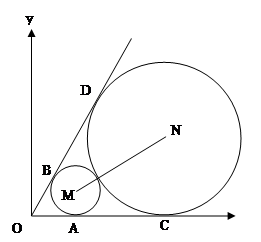
已知函数f(x)=mx2-mx-1.
(1)若对于x∈R,f(x)<0恒成立,求实数m的取值范围;
(2)若对于x∈[1,3],f(x)<5-m恒成立,求实数m的取值范围.