甲、乙两人参加某电视台举办的答题闯关游戏,按照规则,甲先从6道备选题中一次任意抽取3道题,独立作答,然后由乙回答剩余3题,每人答对其中的2题就停止答题,即闯关成功。已知6道备选题中,甲能答对其中的4道题,乙答对每道题的概率都是 .
.
(1)求甲、乙至少有一人闯关成功的概率;
(2)设甲答对题目的个数为 ,求
,求 的分布列及数学期望.
的分布列及数学期望.
(本小题满分12分)
已知数列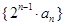 的前
的前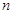 项和
项和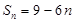 .
.
(Ⅰ)求数列{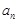 }的通项公式;
}的通项公式;
(Ⅱ)设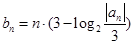 ,求数列{
,求数列{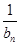 }的前
}的前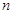 项和.
项和.
(本小题满分10分)
某大学开设甲、乙、丙三门选修课,学生是否选修哪门课互不影响. 已知学生小张只选甲的概率为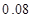 ,只选修甲和乙的概率是
,只选修甲和乙的概率是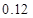 ,至少选修一门的概率是
,至少选修一门的概率是 ,用
,用 表示小张选修的课程门数和没有选修的课程门数的乘积.
表示小张选修的课程门数和没有选修的课程门数的乘积.
(Ⅰ)求学生小张选修甲的概率;
(Ⅱ)记“函数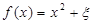
 为
为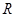 上的偶函数”为事件
上的偶函数”为事件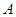 ,求事件
,求事件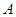 的概率;
的概率;
(Ⅲ)求 的分布列和数学期望;
的分布列和数学期望;
. (本小题满分10分)如图,在三棱锥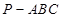 中,
中, 底面
底面 ,点
,点 ,
, 分别在棱
分别在棱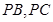 上,且
上,且
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)当 为
为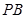 的中点时,求
的中点时,求 与平面
与平面 所成的角的大小;
所成的角的大小;
(Ⅲ)是否存在点 使得二面角
使得二面角 为直二面角?并说明理
为直二面角?并说明理
由.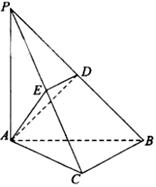
(本小题满分8分)
已知函数 的图像的一部分如图所示。
的图像的一部分如图所示。
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)求函数 的最值;
的最值;
已知函数f(X)=sin2X+acos2X (a R) 且
R) 且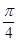 是函数Y=f(X)的零点
是函数Y=f(X)的零点
(1)求a的值,并求函数f(X)的最小正周期
(2)若X 〔0,
〔0,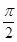 〕,求函数f(X)的值域
〕,求函数f(X)的值域