现有4个人去参加某娱乐活动,该活动有甲、乙两个游戏可供参加者选择,为增加趣味性,约定:每个人通过掷一枚质地均匀的骰子决定自己去参加哪个游戏,掷出点数为1或2的人去参加甲游戏,掷出点数大于2的人去参加乙游戏.
(1)求这4个人中恰有2人去参加甲游戏的概率;
(2)求这4个人中去参加甲游戏的人数大于去参加乙游戏的人数的概率;
(3)用X,Y分别表示这4个人中去参加甲、乙游戏的人数,记ξ=|X Y|,求随机变量ξ的分布列与数学期望Eξ.
已知四边形ABCD满足 ,E是BC的中点,将△BAE沿AE翻折成
,E是BC的中点,将△BAE沿AE翻折成 ,F为
,F为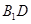 的中点.
的中点.
(1)求四棱锥 的体积;
的体积;
(2)证明: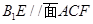 ;
;
(3)求面 所成锐二面角的余弦值.
所成锐二面角的余弦值.
在△ 中,
中,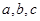 是角
是角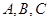 对应的边,向量
对应的边,向量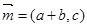 ,
,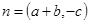 ,且
,且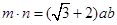 .
.
(1)求角 ;
;
(2)函数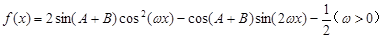 的相邻两个极值的横坐标分别为
的相邻两个极值的横坐标分别为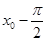 、
、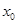 ,求
,求 的单调递减区间.
的单调递减区间.
给定正整数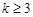 ,若项数为
,若项数为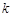 的数列
的数列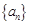 满足:对任意的
满足:对任意的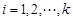 ,均有
,均有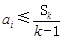 (其中
(其中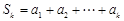 ),则称数列
),则称数列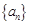 为“Γ数列”.
为“Γ数列”.
(1)判断数列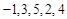 和
和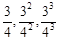 是否是“Γ数列”,并说明理由;
是否是“Γ数列”,并说明理由;
(2)若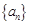 为“Γ数列”,求证:
为“Γ数列”,求证: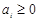 对
对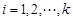 恒成立;
恒成立;
(3)设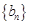 是公差为
是公差为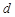 的无穷项等差数列,若对任意的正整数
的无穷项等差数列,若对任意的正整数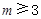 ,
,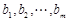
均构成“Γ数列”,求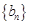 的公差
的公差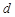 .
.
已知椭圆 的离心率为
的离心率为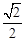 ,短轴端点分别为
,短轴端点分别为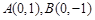 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)若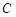 ,
, 是椭圆
是椭圆 上关于
上关于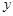 轴对称的两个不同点,直线
轴对称的两个不同点,直线 与
与 轴交于点
轴交于点 ,判断以线段
,判断以线段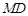 为直径的圆是否过点
为直径的圆是否过点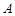 ,并说明理由.
,并说明理由.