在某批次的某种灯泡中，随机地抽取
个样品，并对其寿命进行追踪调查，将结果列成频率分布表如下.根据寿命将灯泡分成优等品、正品和次品三个等级，其中寿命大于或等于
天的灯泡是优等品，寿命小于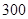
天的灯泡是次品，其余的灯泡是正品.
| 寿命（天） |
频数 |
频率 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
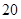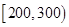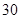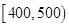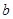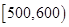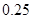| 合计 |
|
 |
（1）根据频率分布表中的数据，写出、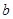的值；
（2）某人从灯泡样品中随机地购买了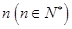
个，如果这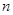
个灯泡的等级情况恰好与按三个等级分层抽样所得的结果相同，求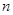的最小值；
（3）某人从这个批次的灯泡中随机地购买了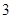
个进行使用，若以上述频率作为概率，用
表示此人所购买的灯泡中次品的个数，求的分布列和数学期望.
(本题满分10分)选修4-1：几何证明与选讲
如图，
为直角三角形，
，以
为直径的圆交
于点
，点
是
边的中点，连
交圆
于点
.
⑴ 求证：
四点共圆；
⑵ 求证：
.
（本小题满分12分）
设函数
.
⑴ 当
时,求函数
在点
处的切线方程；
⑵ 对任意的
函数
恒成立，求实数
的取值范围.
（本小题满分12分）
已知椭圆C：
的离心率为
，且过点Q(1，）．
（1) 求椭圆C的方程；
(2) 若过点M(2，0)的直线与椭圆C相交于A，B两点，设P点在直线
上，且满足
(O为坐标原点），求实数t的最小值．
（本小题满分12分）某单位为了提高员工素质，举办了一场跳绳比赛，其中男员工12人，女员工18人，其成绩编成如图所示的茎叶图（单位：分），分数在175分以上（含175分）者定为“运动健将”，并给予特别奖励，其他人员则给予“运动积极分子”称号.
⑴ 若用分层抽样的方法从“运动健将”和“运动积极分子”中抽取10人，然后再从这10人中选4人，求至少有1人是“运动健将”的概率；
⑵ 若从所有“运动健将”中选3名代表，用
表示所选代表中女“运动健将”的人数，试写出的分布列，并求的数学期望.
（本小题满分12分）在三棱锥
中，
，
，
平面
平面
，
为
的中点.
(1) 证明：
；
(2) 求
所成角的大小.