如图,在直角梯形ABEF中, ,
, ,讲DCEF沿CD折起,使得
,讲DCEF沿CD折起,使得 ,得到一个几何体,
,得到一个几何体,
(1)求证: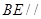 平面ADF;
平面ADF;
(2)求证:AF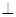 平面ABCD;
平面ABCD;
(3)求三棱锥E-BCD的体积.
已知函数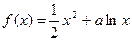 (a∈R).(1)若
(a∈R).(1)若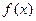 在[1,e]上是增函数,求a的取值范围(2)若a=1,a≤x≤e,证明:
在[1,e]上是增函数,求a的取值范围(2)若a=1,a≤x≤e,证明: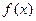 <
<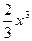
已知函数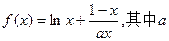 为大于零的常数。
为大于零的常数。

(1)若函数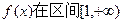 内单调递增,求a的取值范围
内单调递增,求a的取值范围
(2)求函数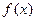 在区间[1,2]上的最小值。
在区间[1,2]上的最小值。
已知函数f(x)= x3-2ax2+3x(x∈R).
x3-2ax2+3x(x∈R).
(1)若a=1,点P为曲线y=f(x)上的一个动点,求以点P为切点的切线斜率取最小值时的切线方程
(2)若函数y=f(x)在(0,+∞)上为单调增函数,试求满足条件的最大整数a.
(本小题满分14分)
已知定义在R上的单调函数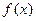 ,存在实数
,存在实数 ,使得对于任意实数
,使得对于任意实数 总有
总有 恒成立.(Ⅰ)求
恒成立.(Ⅰ)求 的值;(Ⅱ)若
的值;(Ⅱ)若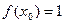 ,且对任意正整数
,且对任意正整数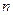 ,有
,有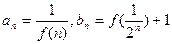 ,记
,记 ,
,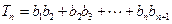 ,比较
,比较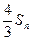 与
与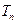 的大小关系;
的大小关系;
(Ⅲ)若不等式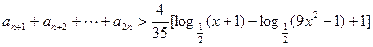 对任意不小于2的正整数
对任意不小于2的正整数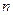 都成立,求
都成立,求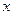 的取值范围.
的取值范围.
(本小题满分13分)
已知函数 R),设关于
R),设关于 的方程
的方程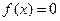 的两实根为
的两实根为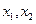 ,方程
,方程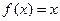 的两实根为
的两实根为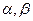 .(Ⅰ)若
.(Ⅰ)若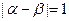 ,求
,求 的关系式;(Ⅱ)若
的关系式;(Ⅱ)若 均为负整数,且
均为负整数,且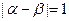 ,求
,求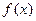 的解析式;(Ⅲ)若
的解析式;(Ⅲ)若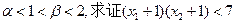 .
.