问题提出：如图①，将一张直角三角形纸片
折叠，使点
与点
重合，这时
为折痕，
为等腰三角形；再继续将纸片沿的对称轴
折叠，这时得到了两个完全重合的矩形（其中一个是原直角三角形的内接矩形，另一个是拼合成的无缝隙、无重叠的矩形），我们称这样两个矩形为“叠加矩形”.
知识运用：
（1）如图②，正方形网格中的能折叠成“叠加矩形”吗？如果能，请在图②中画出折痕；
（2）如图③，在正方形网格中，以给定的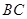
为一边，画出一个斜三角形
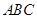，使其顶点在格点上，且折成的“叠加矩形”为正方形；
（3）若一个锐角三角形所折成的“叠加矩形”为正方形，那么它必须满足的条件是什么？结合图③，说明理由。
拓展应用：
（4）如果一个四边形一定能折成"叠加矩形",那么它必须满足的条件是什么？
已知反比例函数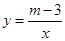
与一次函数y＝3x－m，当
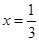时，这两个函数的函数值相等，求这两个函数的解析式．
已知y与x成反比例，且当x＝－3时，y＝7，求y关于x的函数解析式．
已知y是x的反比例函数，且x＝2时，y＝－3，确定此函数的解析式，并求当y＝－8时，自变量x的值．
已知：
．
（1）当m为何值时，y是x的正比例函数？
（2）当m为何值时，y是x的二次函数？
（3）当m为何值时，y是x的反比例函数？
在平面直角坐标系中，我们不妨把横坐标与纵坐标相等的点称为“梦之点”．例如点（－1，－1），（0，0），（
，），……都是“梦之点”，显然，这样的“梦之点”有无数个．
（1）若点P（2，m）是反比例函数
（n为常数，n≠0）的图象上的“梦之点”，求这个反比例函数的解析式；
（2）函数y＝3kx＋s－1（k，s是常数）的图象上存在“梦之点”吗？若存在，请求出“梦之点”的坐标；若不存在，请说明理由；
（3）若二次函数y＝ax2＋bx＋1（a，b是常数，a＞0）的图象上存在两个不同的“梦之点”A（x1，y1），B（x2，y2），且满足－2＜x1＜2，|x1－x2|＝2，令
，试求t的取值范围．