如图所示，一次函数y=k1x+b与反比例函数y=
(x<0)的图象相交于A，B两点，且与坐标轴的交点为(–6,0)，(0,6)，点B的横坐标为–4．
（1）试确定反比例函数的解析式；
（2）求△AOB的面积；
（3）直接写出不等式k1x+b>的解．
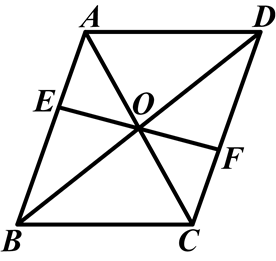
在□ABCD中，对角线AC、BD交于点O，过点O作直线EF分别交线段AD、BC于点E、F．
(1)根据题意，画出图形，并标上正确的字母；
(2)求证：DE＝BF．
如图，已知四边形ABCD是平行四边形，点E、B、D、F在同一直线上，且BE＝DF．求证：AE＝CF．
如图，在□ABCD中，E、F是对角线BD上的两点，且BE＝DF，连接AE、CF．请你猜想：AE与CF有怎样的数量关系，并对你的猜想加以证明．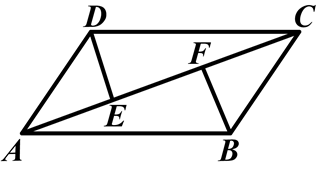
如图，在平行四边形ABCD中，DE⊥AB于E，DF⊥BC于F，平行四边形ABCD的周长为48，DE＝5，DF＝10．
(1)求AB的长度；
(2)求平行四边形ABCD的面积．
如图，平行四边形ABCD的对角线AC，BD相交于点O，EF过点O且与AB、CD分别交于点E，F，求证：△AOE≌△COF．