如图所示为某娱乐场的一种游戏装置的滑道示意图,其中AB为曲面滑道,BC为长28m水平滑道,动摩擦因数为0.2;水平滑道BC与半径为10m的四分之一圆弧滑道CD相切,DE为水池的水平面,水池足够深,以确保人落水后的安全。某人坐滑车从坡顶的A点由静止滑下,经过高度差为20m的B点时的速度为16 m/s,最后落在水面上。人和滑车的质量共为70kg,将人和滑车作为质点处理,g取l0rn/s2。问:
(1)从A到B的过程中,人的机械能是否守恒,
(2)到达C点时的速度为多少?
(3)落水点与C点的水平距离。
如右图,质量分别为m和M的两个星球A和B在引力作用下都绕O点做匀速圆周运动,星球A和B两者中心之间的距离为L.已知A、B的中心和O三点始终共线,A和B分别在O的两侧.引力常数为G.
(1)求两星球做圆周运动的周期;
(2)在地月系统中,若忽略其它星球的影响,可以将月球和地球看成上述星球A和B,月球绕其轨道中心运行的周期记为 .但在近似处理问题时,常常认为月球是绕地心做圆周运动的,这样算得的运行周期记为
.但在近似处理问题时,常常认为月球是绕地心做圆周运动的,这样算得的运行周期记为 .已知地球和月球的质量分别为
.已知地球和月球的质量分别为 和
和 .求
.求 与
与 两者平方之比.(结果保留3位小数)
两者平方之比.(结果保留3位小数)
质量为m的钢板与直立轻弹簧的上端连接,弹簧下端固定在地上.平衡时,弹簧的压缩量为x0,如右图所示.一物块从钢板正上方距离为3x0的A处自由落下,打在钢板上并立刻与钢板一起向下运动,但不粘连.它们到达最低点后又向上运动.已知物块质量也为m时,它们恰能回到O点.若物块质量为2m,仍从A处自由落下,则物块与钢板回到O点时,还具有向上的速度.求物块向上运动到达的最高点与O点的距离.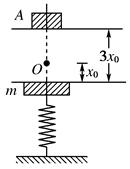
如下图所示,木块A、B的质量均为m,放在一段粗糙程度相同的水平地面上,木块A、B间夹有一小块炸药(炸药的质量可以忽略不计).让A、B以初速度 一起从O点滑出,滑行一段距离后到达P点,速度变为
一起从O点滑出,滑行一段距离后到达P点,速度变为 ,此时炸药爆炸使木块A、B脱离,发现木块B立即停在原位置,木块A继续沿水平方向前进.已知O、P两点间的距离为s,炸药爆炸时释放的化学能均全部转化为木块的动能,爆炸时间很短可以忽略不计.求:
,此时炸药爆炸使木块A、B脱离,发现木块B立即停在原位置,木块A继续沿水平方向前进.已知O、P两点间的距离为s,炸药爆炸时释放的化学能均全部转化为木块的动能,爆炸时间很短可以忽略不计.求:
(1)木块与水平地面的动摩擦因数μ;
(2)炸药爆炸时释放的化学能.
在核反应堆中,常用减速剂使快中子减速.假设减速剂的原子核质量是中子的k倍,中子与原子核的每次碰撞都可看成是弹性正碰.设每次碰撞前原子核可认为是静止的,求N次碰撞后中子速率与原速率之比.
某公共汽车的运行非常规则,先由静止开始匀加速启动,当速度达到v1=10 m/s时再做匀速运动,进站前开始匀减速制动,在到达车站时刚好停住.公共汽车在每个车站停车时间均为Δt=25 s,然后以同样的方式运行至下一站.已知公共汽车在加速启动和减速制动时加速度大小都为a=1 m/s2,而所有相邻车站间的行程都为x=600 m.有一次当公共汽车刚刚抵达一个车站时,一辆电动车刚经过该车站一段时间t0=60 s,已知该电动车速度大小恒定为v2=6 m/s,而且行进路线、方向与公共汽车完全相同,不考虑其他交通状况的影响,试求:
(1)公共汽车从其中一车站出发至到达下一站所需的时间t;
(2)若从下一站开始计数,公共汽车在刚到达第n站时,电动车也恰好同时到达此车站,n为多少?