从数列 中抽出一些项,依原来的顺序组成的新数列叫数列
中抽出一些项,依原来的顺序组成的新数列叫数列 的一个子列.
的一个子列.
(1)写出数列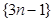 的一个是等比数列的子列;
的一个是等比数列的子列;
(2)若 是无穷等比数列,首项
是无穷等比数列,首项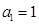 ,公比
,公比 且
且 ,则数列
,则数列 是否存在一个子列
是否存在一个子列
为无穷等差数列?若存在,写出该子列的通项公式;若不存在,证明你的结论.
已知数列 的前n项和
的前n项和 (其中c,k为常数),且
(其中c,k为常数),且 2=4,
2=4, 6=8
6=8 3
3
(Ⅰ)求 ;
;
(Ⅱ)求数列 的前n项和Tn.
的前n项和Tn.
(本小题满分14分)已知焦点在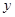 轴,顶点在原点的抛物线
轴,顶点在原点的抛物线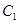 经过点
经过点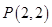 ,以抛物线
,以抛物线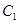 上一点
上一点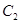 为圆心的圆过定点
为圆心的圆过定点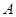 (0,1),记
(0,1),记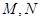 为圆
为圆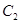 与
与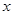 轴的两个交点.
轴的两个交点.
(1)求抛物线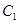 的方程;
的方程;
(2)当圆心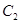 在抛物线上运动时,试判断
在抛物线上运动时,试判断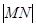 是否为一定值?请证明你的结论;
是否为一定值?请证明你的结论;
(3)当圆心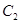 在抛物线上运动时,记
在抛物线上运动时,记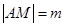 ,
,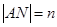 ,求
,求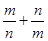 的最大值.
的最大值.
(本小题满分13分)已知函数 ,其中
,其中 为常数.
为常数.
(1)当 时,若
时,若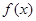 在区间
在区间 上的最大值为
上的最大值为 ,求
,求 的值;
的值;
(2)当 时,若函数
时,若函数 存在零点,求实数
存在零点,求实数 的取值范围.
的取值范围.
(本小题满分12分)如图,四棱锥 的底面是正方形,
的底面是正方形, ⊥底面
⊥底面 ,点
,点 在棱
在棱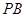 上.
上.
(Ⅰ)求证:平面 ⊥平面
⊥平面 ;
;
(Ⅱ)当 且
且 为
为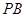 的中点时,求
的中点时,求 与平面
与平面 所成角的正弦值.
所成角的正弦值.
(本小题满分12分)已知各项都不相等的等差数列{an}的前六项和为60,且a6为a1和a21的等比中项.
(1)求数列{an}的通项公an及前n项和Sn;
(2)若数列{bn}满足bn+1-bn=an(n∈N*),且b1=3,求数列{}的前n项和Tn.