甲乙两个同学进行定点投篮游戏,已知他们每一次投篮投中的概率均为 ,且各次投篮的结果互不影响.甲同学决定投5次,乙同学决定投中1次就停止,否则就继续投下去,但投篮次数不超过5次.
,且各次投篮的结果互不影响.甲同学决定投5次,乙同学决定投中1次就停止,否则就继续投下去,但投篮次数不超过5次.
(1)求甲同学至少有4次投中的概率;
(2)求乙同学投篮次数 的分布列和数学期望.
的分布列和数学期望.
设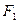 、
、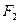 分别是椭圆
分别是椭圆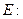
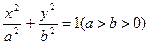 的左、右焦点,过
的左、右焦点,过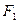 且斜率为
且斜率为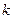 的直线
的直线 与
与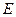 相交于
相交于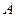 、
、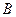 两点,且
两点,且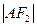 、
、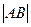 、
、 成等差数列.
成等差数列.
(1)若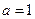 ,求
,求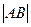 的值;
的值;
(2)若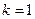 ,设点
,设点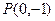 满足
满足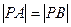 ,求椭圆
,求椭圆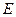 的方程.
的方程.
已知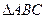 的两个顶点为
的两个顶点为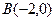 ,
,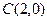 ,周长为12.
,周长为12.
(1)求顶点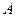 的轨迹
的轨迹 方程;
方程;
(2)若直线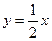 与点
与点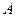 的轨迹
的轨迹 交于
交于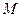 、
、 两点,求
两点,求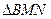 的面积.
的面积.
已知抛物线关于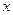 轴对称,顶点在坐标原点,点
轴对称,顶点在坐标原点,点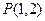 ,
,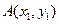 ,
,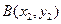 均在抛物线上.
均在抛物线上.
(1)求抛物线方程及准线方程;
(2)若点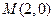 在
在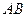 上,求
上,求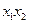 、
、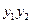 的值.
的值.
某突发事件,在不采取任何预防措施的情况下发生的概率为0.3,一旦发生,将造成400万元的损失.现有甲、乙两种相互独立的预防措施可供采用.单独采用甲、乙预防措施所需的费用分别为45万元和30万元,采用相应预防措施后此突发事件不发生的概率为0.9和0.85.若预防方案允许甲、乙两种预防措施单独采用、联合采用或不采用,请确定预防方案使总费用最少.(总费用=采取预防措施的费用+发生突发事件损失的费用)
已知8个球队中有3个弱队,以抽签方式将这8个球队分为A、B两组,每组4个.求
(Ⅰ)A、B两组中有一组恰有两个弱队的概率;
(Ⅱ)A组中至少有两个弱队的概率.