如图，在直角梯形ABCP中，
,D是AP的中点，E,G分别为PC,CB的中点，将三角形PCD沿CD折起，使得PD垂直平面ABCD.（1）若F是PD的中点，求证：AP
平面EFG;（2）当二面角G-EF-D的大小为
时，求FG与平面PBC所成角的余弦值.
已知函数
在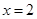
处有极大值．
（1）当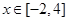
时，函数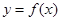
的图象在抛物线
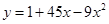的下方，求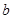
的取值范围．
（2）若过原点有三条直线与曲线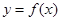相切，求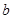的取值范围；
等差数列
的首项为23，公差为整数，且第6项为正数，从第7项起为负数。
（1）求此数列的公差d；
（2）当前n项和
是正数时，求n的最大值。
已知向量
，设函数
（1）求
在区间
上的零点；
（2）在
中，角
的对边分别是
，且满足
，求
的取值范围．
已知
（1）求函数
的最小正周期及在区间
上的最大值和最小值；
（2）若
，
，求
的值．
设椭圆
的左、右焦点分别为
，上顶点为
，在
轴负半轴上有一点
，满足
，且
．
（1）求椭圆
的离心率；
（2）若过
三点的圆与直线
相切，求椭圆的方程；
（3）在（2）的条件下，过右焦点
作斜率为
的直线
与椭圆交于
两点，线段
的中垂线与轴相交于
，求实数
的取值范围．