设椭圆 的左、右焦点分别为
的左、右焦点分别为 ,上顶点为
,上顶点为 ,在
,在 轴负半轴上有一点
轴负半轴上有一点 ,满足
,满足 ,且
,且 .
.
(1)求椭圆 的离心率;
的离心率;
(2)若过 三点的圆与直线
三点的圆与直线 相切,求椭圆
相切,求椭圆 的方程;
的方程;
(3)在(2)的条件下,过右焦点 作斜率为
作斜率为 的直线
的直线 与椭圆
与椭圆 交于
交于 两点,线段
两点,线段 的中垂线与
的中垂线与 轴相交于
轴相交于 ,求实数
,求实数 的取值范围.
的取值范围.
(本小题满分13分)已知函数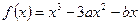 ,其中
,其中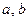 为实数.
为实数.
(Ⅰ) 若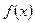 在
在 处取得的极值为
处取得的极值为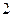 ,求
,求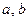 的值;
的值;
(Ⅱ)若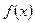 在区间
在区间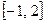 上为减函数,且
上为减函数,且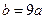 ,求
,求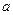 的取值范围.
的取值范围.
(本小题满分12分) 某租赁公司拥有汽车100辆.当每辆车的月租金为3000元时,可全 部租出.当每辆车的月租金每增加50元时,未租出的车将会增加一辆.租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.
部租出.当每辆车的月租金每增加50元时,未租出的车将会增加一辆.租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.
(1)当每辆车的月租金定为3600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
(本小题满分12分)在△ABC中,已知B=45°,D是BC边上的一点,
AD=10,AC=14,DC=6 ,求AB的长.
,求AB的长.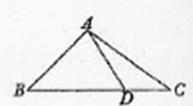
(本小题满分12分) 已知函数
(Ⅰ)将函数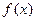 化简成
化简成 的形式,并指出
的形式,并指出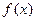 的最小正周期;
的最小正周期;
(Ⅱ)求函数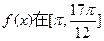 上的最大值和最小值
上的最大值和最小值
(本小题满分12分)已知向量 与
与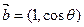 互相垂直,其中
互相垂直,其中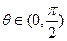 .
.
(1)求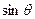 和
和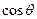 的值;
的值;
(2)若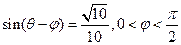 ,求
,求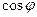 的值.
的值.