如图,四边形为边长为a的正方形,以D为圆心,DA为半径的圆弧与以BC为直径的圆O交于F,连接CF并延长交AB于点E.
(1).求证:E为AB的中点;
(2).求线段FB的长.
(12分)（1）已知
，求
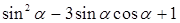的值；
（2）求函数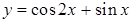
的值域．
（本小题满分14分）
已知二次函数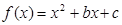
的图象过点
，且函数对称轴方程为
.
（Ⅰ）求函数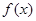
的解析式；
（Ⅱ）设函数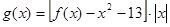
，求
在区间
上的最小值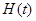
；
（Ⅲ）探究：函数
的图象上是否存在这样的点，使它的横坐标是正整数，纵坐标是一个完全平方数？如果存在，求出这样的点的坐标；如果不存在，请说明理由.
（本小题满分12分）
已知函数
的定义域是
，对于任意的
，有
，且当
时，
．
（Ⅰ）验证函数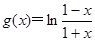
是否满足上述这些条件；
（Ⅱ）你发现这样的函数还具有其它什么样的主要性质？试就函数的奇偶性、单调性的结论写出来，并加以证明．
（本小题满分12分）
某车间生产一种仪器的固定成本是10000元，每生产一台该仪器需要增加投入100元，已知总收入满足函数：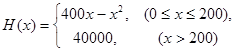
，其中
是仪器的月产量（总收入＝总成本＋利润）．
（Ⅰ）将利润（用
表示）表示为月产量的函数；
（Ⅱ）当月产量为何值时，车间所获利润最大？最大利润是多少元？
（本小题满分12分）
已知函数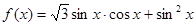
.
（Ⅰ）求函数
的最小正周期和单调递增区间；
（Ⅱ）函数的图象可由函数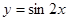
的图象经过怎样的变换得出？