已知四棱锥P-ABCD中,PB⊥平面ABCD,底面ABCD是直角梯形,∠ABC=∠BCD=90°,PB=BC=CD= AB.Q是PC上的一点,且PA∥平面QBD.
AB.Q是PC上的一点,且PA∥平面QBD.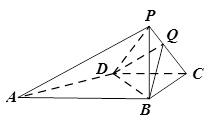
⑴确定Q的位置;
⑵求二面角Q-BD-C的平面角的余弦值.
已知各项不为零的数列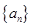 的前
的前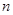 项和为
项和为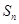 ,且满足
,且满足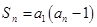 ,数列
,数列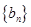 满足
满足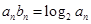 ,数列
,数列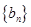 的前
的前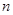 项和
项和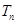
(Ⅰ)求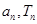
(Ⅱ)若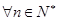 ,不等式
,不等式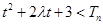 恒成立,求使关于
恒成立,求使关于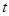 的不等式有解的充要条件.
的不等式有解的充要条件.
在如图所示的几何体中, △ABC为正三角形,AE和CD都垂直于平面ABC,且AE=AB=2,CD=1,F为BE的中点.
(Ⅰ)求证:平面DBE⊥平面ABE;
(Ⅱ)求直线BD和平面ACDE所成角的余弦值.
已知向量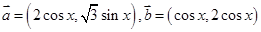 ,函数
,函数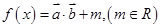 ,且当
,且当 时,
时,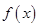 的最小值为2
的最小值为2
(Ⅰ)求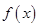 的单调递增区间;
的单调递增区间;
(Ⅱ)先将函数 的图象上的点纵坐标不变,横坐标缩小到原来的
的图象上的点纵坐标不变,横坐标缩小到原来的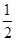 ,再把所得的图象向右平移
,再把所得的图象向右平移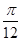 个单位,得到函数
个单位,得到函数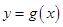 的图象,求方程
的图象,求方程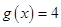 在区间
在区间 上所有根之和.
上所有根之和.
设函数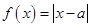
(Ⅰ)当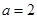 时,解不等式
时,解不等式 ;
;
(Ⅱ)若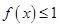 的解集为
的解集为 ,
, 求证:
求证:
已知圆 的参数方程是
的参数方程是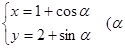 为参数).
为参数).
(Ⅰ)以直角坐标系的原点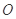 为极点,
为极点, 轴的正半轴为极轴建立极坐标系,写出圆
轴的正半轴为极轴建立极坐标系,写出圆 的极坐标方程;
的极坐标方程;
(Ⅱ)若直线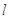 的极坐标方程为
的极坐标方程为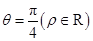 ,设直线
,设直线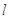 和圆
和圆 的交点为
的交点为 ,求
,求 的面积.
的面积.