函数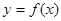 的定义域为
的定义域为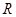 ,若存在常数
,若存在常数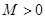 ,使得
,使得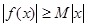 对一切实数
对一切实数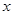 均成立,则称
均成立,则称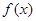 为“圆锥托底型”函数.
为“圆锥托底型”函数.
(1)判断函数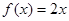 ,
,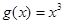 是否为“圆锥托底型”函数?并说明理由.
是否为“圆锥托底型”函数?并说明理由.
(2)若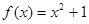 是“圆锥托底型” 函数,求出
是“圆锥托底型” 函数,求出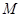 的最大值.
的最大值.
(3)问实数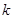 、
、 满足什么条件,
满足什么条件,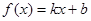 是“圆锥托底型” 函数.
是“圆锥托底型” 函数.
(本小题满分7分)选修4—5:不等式选讲
已知实数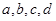 满足
满足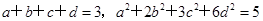 ,
,
求证:(Ⅰ)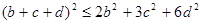 ;
;
(Ⅱ)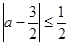 .
.
(本小题满分7分)《选修4-4:坐标系与参数方程》
在直角坐标系中,以坐标原点为极点,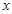 轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为
轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为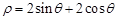 ,曲线D的参数方程为
,曲线D的参数方程为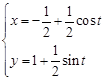 (
(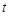 为参数).
为参数).
(Ⅰ)把C的极坐标方程化为直角坐标方程;
(Ⅱ)判定曲线C与曲线D间的位置关系.
(本小题满分7分)选修4—2:矩阵与变换
已知直线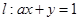 在矩阵
在矩阵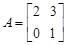 对应的变换作用下变为直线
对应的变换作用下变为直线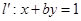 .
.
(Ⅰ)求实数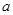 ,
,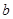 的值;
的值;
(Ⅱ)若点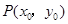 在直线
在直线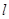 上,且
上,且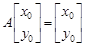 ,求点
,求点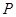 的坐标.
的坐标.
已知点 、
、 为双曲线
为双曲线 :
:
 的左、右焦点,过
的左、右焦点,过 作垂直于
作垂直于 轴的直线,在
轴的直线,在 轴上方交双曲线
轴上方交双曲线 于点
于点 ,且
,且 ,圆
,圆 的方程是
的方程是 .
.
(1)求双曲线 的方程;
的方程;
(2)过双曲线 上任意一点
上任意一点 作该双曲线两条渐近线的垂线,垂足分别为
作该双曲线两条渐近线的垂线,垂足分别为 、
、 ,求
,求 的值;
的值;
(3)过圆 上任意一点
上任意一点 作圆
作圆 的切线
的切线 交双曲线
交双曲线 于
于 、
、 两点,
两点, 中点为
中点为 ,求证:
,求证: .
.
已知函数
(1)讨论 的单调性.
的单调性.
(2)证明: (
( ,e为自然对数的底数)
,e为自然对数的底数)