设数列 ,
, ,
, ,已知
,已知 ,
, ,
, ,
, ,
, ,
, (
( ).
).
(1)求数列 的通项公式;
的通项公式;
(2)求证:对任意 ,
, 为定值;
为定值;
(3)设 为数列
为数列 的前
的前 项和,若对任意
项和,若对任意 ,都有
,都有 ,求实数
,求实数 的取值范围.
的取值范围.
等比数列{ }的前n项和为
}的前n项和为 ,已知对任意的
,已知对任意的 ,点
,点 ,均在函数
,均在函数 且
且 均为常数)的图像上.
均为常数)的图像上.
(1)求r的值;
(2)当b=2时,记  求数列
求数列 的前
的前 项和
项和 .
.
已知 ,且
,且 .
.
(1)将 表示为
表示为 的函数
的函数 ,并求
,并求 的单调增区间;
的单调增区间;
(2)已知 分别为
分别为 的三个内角
的三个内角 对应的边长,若
对应的边长,若 ,求
,求 的面积.
的面积.
已知an是一个等差数列,且a2=18,a14=—6.
(1)求an的通项an;
(2)求an的前n项和Sn的最大值并求出此时n值.
设a为实数,记函数 的最大值为
的最大值为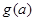 .
.
(1)设t= ,求t的取值范围,并把f(x)表示为t的函数m(t) ;
,求t的取值范围,并把f(x)表示为t的函数m(t) ;
(2)求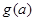 ;
;
(3)试求满足 的所有实数a.
的所有实数a.
设函数 .
.
(1)在区间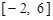 上画出函数
上画出函数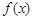 的图象 ;
的图象 ;
(2)设集合 . 试判断集合
. 试判断集合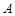 和
和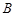 之间
之间
的关系,并给出证明 ;
(3)当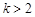 时,求证:在区间
时,求证:在区间 上,
上,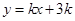 的图象位于函数
的图象位于函数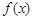 图象的上方.
图象的上方.