(10内江21)下列相关化学用语的表达正确的是
| A.两个镁离子:2Mg2+ | B.四个氢氧根离子:4OH |
| C.氧化铝中铝元素的化合价:Al3+ | D.纯碱的化学式NaCO3 |
(10内江17)一直氯原子结构示意图为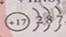 ,下列叙述错误的是
,下列叙述错误的是
| A.氯原子核内有17个质子 |
| B.氯原子核外有三个电子层 |
| C.氯原子核内有17个中子 |
| D.氯原子溶液得到一个电子形成氯离子 |
(10日照19)自2010年4月1日始,我国对酒后驾驶进行了专项整治。交警用装有重铬酸钾(K2Cr2O7)的检测仪,来检测司机是否酒后驾车。其原理是红色的重铬酸钾遇酒精后生成蓝绿色的物质。下列说法不正确的是
| A.重铬酸钾是由三种元素组成的 |
| B.该变化是化学变化 |
| C.重铬酸钾的相对分子质量是294 |
| D.组成重铬酸钾的各元素个数比为2:2:7 |
(10日照12)某建筑工地发生多人食物中毒,经化验为误食工业用盐亚硝酸钠(NaNO2)所致,NaNO2中氮元素的化合价是
| A.+2 | B.+3 | C.+4 | D.+5 |
(10日照3)下列物质中存在氧分子的是
| A.水 | B.双氧水 | C.二氧化碳 | D.液态氧 |