如图，四棱锥P—ABCD中，PD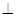
底面ABCD，AB//DC，AD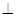DC，AB=AD=1，DC=2，PD=
，M为棱PB的中点．
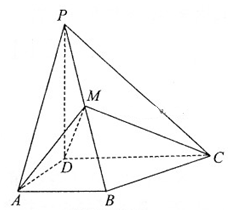
(1)证明：DM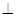平面PBC；
(2)求二面角A—DM—C的余弦值．
在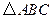
中，已知
，
，
．
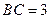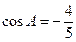（1）求
的值；（2）求
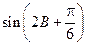的值．
现有编号分别为1，2，3，4，5，6，7，8，9的九道不同的数学题。某同学从这九道题中一次随机抽取两道题，每题被抽到的概率是相等的，用符号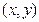
表示事件“抽到两 题的编号分别为
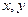,且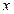
＜
”。
（1）共有多少个基本事件？并列举出来。
（2）求该同学所抽取的两道题的编号之和小于17但不小于11的概率
抛物线
的准线的方程为
，该抛物线上的每个点到准线的距离都与到定点
的距离相等，圆是以为圆心，同时与直线
和
相切的圆，
（Ⅰ）求定点的坐标；
（Ⅱ）是否存在一条直线
同时满足下列条件：
①分别与直线
和
交于
、
两点，且
中点为
；
②被圆截得的弦长为2．
如图所示, 四棱锥P
ABCD底面是直角梯形, 
底面ABCD, E为PC的中点, PA＝AD＝AB＝1. 
（1）证明: 
;
（2）证明: 
;
（3）求三棱锥BPDC的体积V.
设
，函数
．
（Ⅰ）若
是函数
的极值点，求
的值；
（Ⅱ）若函数
，在
处取得最大值，求
的取值范围．