某公司承建扇环面形状的花坛如图所示,该扇环面花坛是由以点 为圆心的两个同心圆弧
为圆心的两个同心圆弧 、弧
、弧 以及两条线段
以及两条线段 和
和 围成的封闭图形.花坛设计周长为30米,其中大圆弧
围成的封闭图形.花坛设计周长为30米,其中大圆弧 所在圆的半径为10米.设小圆弧
所在圆的半径为10米.设小圆弧 所在圆的半径为
所在圆的半径为 米(
米( ),圆心角为
),圆心角为 弧度.
弧度.
(1)求 关于
关于 的函数关系式;
的函数关系式;
(2)在对花坛的边缘进行装饰时,已知两条线段的装饰费用为4元/米,两条弧线部分的装饰费用为9元/米.设花坛的面积与装饰总费用的比为 ,当
,当 为何值时,
为何值时, 取得最大值?
取得最大值?
已知抛物线 :
: (
( ),焦点为
),焦点为 ,直线
,直线 交抛物线
交抛物线 于
于 、
、 两
两
点, 是线段
是线段 的中点,过
的中点,过 作
作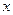 轴的垂线交抛物线
轴的垂线交抛物线 于点
于点 ,
,
(1)若抛物线 上有一点
上有一点 到焦点
到焦点 的距离为
的距离为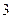 ,求此时
,求此时 的值;
的值;
(2)是否存在实数 ,使
,使 是以
是以 为直角顶点的直角三角形?若存在,求出
为直角顶点的直角三角形?若存在,求出 的值;若不存在,说明理由。
的值;若不存在,说明理由。
如图,函数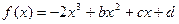 图像与x轴相切于原点。
图像与x轴相切于原点。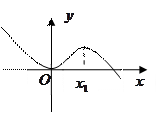
(1)求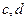 的值;
的值;
(2)若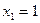 ,设
,设 ,若在
,若在 上至少存在一点
上至少存在一点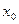 ,使得
,使得 成立,求实数
成立,求实数 的取
的取 值范围.
值范围.
已知椭圆 的离心率为
的离心率为 ,点
,点 是椭圆上一定点,直线
是椭圆上一定点,直线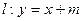 交椭圆于不同的两点
交椭圆于不同的两点 、
、 .
.
(1)求椭圆方程
(2)求 的取值范围.
的取值范围.
已知命题 :“椭圆
:“椭圆 的焦点在x轴上” ,命题
的焦点在x轴上” ,命题 :只有一个实数
:只有一个实数 满足不等式
满足不等式 . 若命题“p且q”是真命题,求实数a的值
. 若命题“p且q”是真命题,求实数a的值 .
.
已知x=2是函数 的一个极值点.(Ⅰ)求
的一个极值点.(Ⅰ)求 ;(Ⅱ)求函数
;(Ⅱ)求函数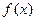 的单调区间;(Ⅲ)若直线
的单调区间;(Ⅲ)若直线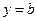 与函数
与函数 的图像有
的图像有 个交点,求
个交点,求 的取值范围.
的取值范围.