（本小题满分15分）
已知椭圆C：＋＝1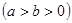
的离心率为，左焦点为F(－1，0)，
(1) 设A，B分别为椭圆的左、右顶点，过点F且斜率为k的直线L与椭圆C交于M，N两点，若
，求直线L的方程；
(2)椭圆C上是否存在三点P，E，G，使得S△OPE＝S△OPG＝S△OEG＝？
（本小题满分12分）在△ABC中，角A，B，C的对边分别为a，b，c，已知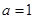
，A＝
，
．
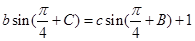（1）求B，C的值；
（2）求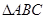
的面积．
（本小题满分一10分）【选修4一5：不等式选讲】
已知
（1）求不等式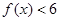
的解集；
（2）设m，n，p为正实数，且
，求证：
．
（本小题满分10分）【选修4一4：坐标系与参数方程】
已知在直角坐标系x0y中，曲线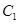
：
（
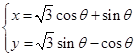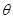为参数），在以平面直角坐标系的原点）为极点，x轴的正半轴为极轴，取相同单位长度的极坐标系中，曲线
：
．
（1）求曲线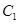的普通方程和曲线的直角坐标方程；
（2）曲线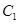上恰好存在三个不同的点到曲线的距离相等，分别求这三个点的极坐标．
（本小题满分10分）【选修4一1：几何证明选讲】
如图，已知AB是圆O的一条弦，延长AB到点C使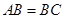
，过点B作
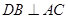且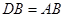
，连接DA与圆O交于点E，连接CE与圆O交于点F．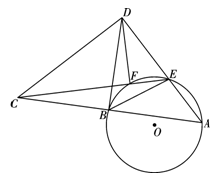
（1）求证：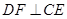
；
（2）若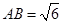
，
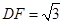，求BE．
（本小题满分12分）已知函数
，
．
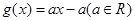（1）若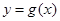
为曲线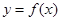
的一条切线，求a的值；
（2）已知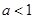
，若存在唯一的整数
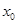使得
，求a的取值范围．